Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Who will win in the race between two cars, one with a conventional internal-combustion engine, the other with an electric engine?
Why did the car with the electric engine win? The answer has to do with the relationship between power, torque, and angular velocity.
Remember that the work done on an object by a rotating engine depends on a particular combination of torque and angular velocity:
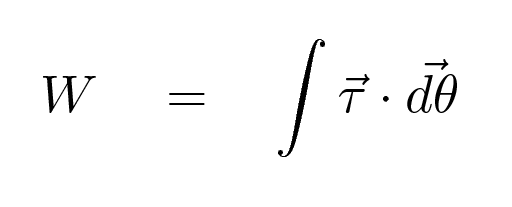
The RATE at which work is done on an object is simply the derivative of work with respect to time. That is, the instantaneous power delivered by an engine will be
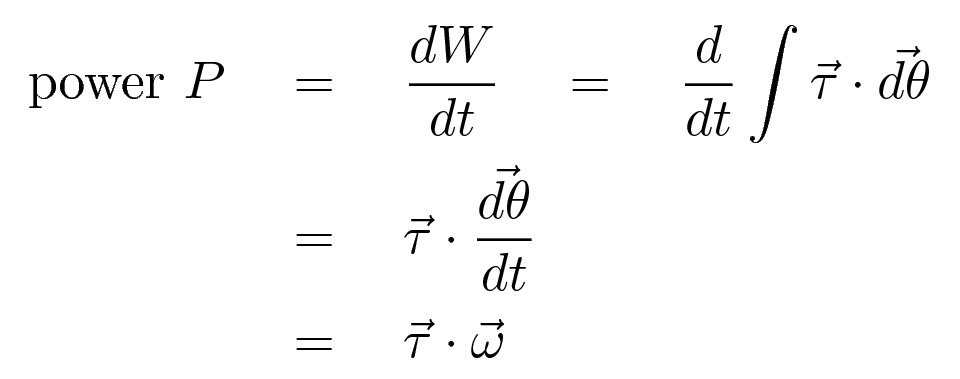
So, let's look at how the torque of a typical internal-combustion engine varies with the angular velocity of the engine.
At very low engine (rotational) speeds, the torque falls off rapidly. The peak torque occurs when the engine is spinning very rapidly.
But, of course, when a car is sitting still, the engine is NOT spinning rapidly. In fact, when the transmission is initially put into gear, it has to force the wheels to start spinning from rest -- which means that the engine will begin at a very low rotational speed.
Q: Can you compute the instantaneous power of
this engine at
1000 RPM
2000 RPM
4000 RPM
Let's compare those values to the amount of energy needed to change the speed of an automobile by some small amount. Consider the 2003 Corvette LS1, which has a mass M = 1458 kg, as it accelerates from a standing start:
change in speed
0 - 10 mph 20 - 30 mph 50 - 60 mph
-------------------------------------------------------------------------
m/s m/s m/s
-------------------------------------------------------------------------
Kinetic start
Energy
(J) end
change
-------------------------------------------------------------------------
The table above tells you how much energy it takes to increase the speed of the car in various intervals. Now, the amount of energy delivered by an engine is
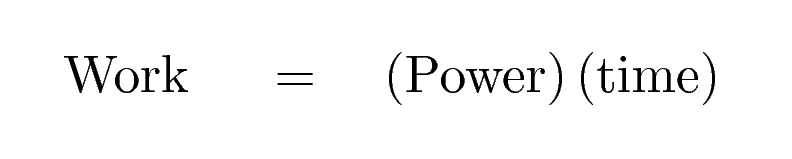
So, how long will it take the internal combustion engine to deliver enough energy to increase the car's speed over each of these intervals? We'll make the simplifying assumption that over each of the intervals, the power delivered remains constant; I'll pick some representative engine rotational speeds.
change in speed
0 - 10 mph 20 - 30 mph 50 - 60 mph
-------------------------------------------------------------------------
approx engine
speed (RPM) 1000 2000 4000
-------------------------------------------------------------------------
Work (J)
Power (W)
time
required (s)
-------------------------------------------------------------------------
The Corvette actually accelerates from 0 - 60 mph in about 4.5 seconds. All our calculations have assumed perfect efficiency and no losses; in real life, some 10 percent or so of the power delivered by the engine is lost to friction and heat in the transmission before it reaches the wheels.
But what about electric engines? The key factor is the relationship between torque and engine speed: in an electric engine (also called an "electric motor"), the torque is largely independent of rotational speed. For example, the Tesla Roadster has an engine with this profile:
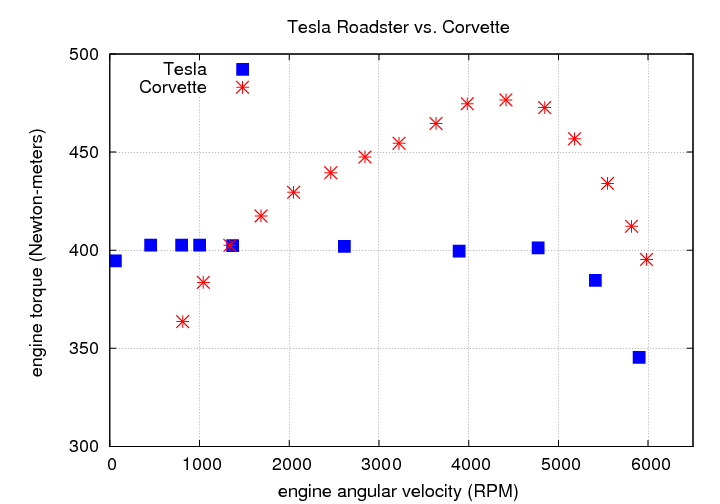
The electric engine produces maximum torque even when the rotational velocity is very small. This has several consequences:
Yes, that's right: an electric car doesn't need gears! Read about this and other features of an electric engine in a description of the Tesla Roadster's engine.
Of course, there are some complications -- there's no such thing as a free lunch, after all. In order to produce this performance, the currents running through an electric motor have to be pretty large:
For more information
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.