Physics 212, Quiz #7b: Jan 12, 1998

Show all work -- you may receive partial credit!

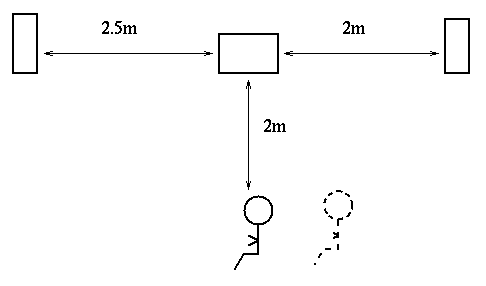
Joe unpacks his stereo system. He places the amplifier on his table, one speaker 2.5 m to its left, and the other speaker 2.0 m to its right. Joe then sits in a chair, 2.0 m in front of the amplifier.

Question 1: Draw a picture showing a view from above of Joe, the amplifier, and both speakers.

Question 2: What is the distance from Joe to the left-hand speaker, and from Joe to the right-hand speaker?

  Answer:  distance Joe to left speaker is

              d(left)  = sqrt( [2m]^2 + [2.5m]^2 ) = 3.20 m

           distance Joe to right speaker is

              d(right) = sqrt( [2m]^2 + [2m]^2 )   = 2.83 m

Assume that sound travels at v = 343 m/s. The speakers play a note with frequency f = 463.5 Hz.

Question 3: Does Joe hear constructive or destructive interference? Why?

  Answer: the wavelength of this sound is

                         v    343 m/s
               lambda = --- = -------- = 0.740 m
                         f    463.5 Hz 


          The difference in path length from Joe to the two speakers is

                 d(left) - d(right) =  3.20 m - 2.83 m = 0.37 m

                                    = lamba / 2

          Since the difference in path length is 1/2 of a wavelength,
          the interference will be destructive.

Joe moves his chair sideways 0.25 m to the right.

Question 4: What sort of interference does he now hear? Why?

  Answer: at his new position (dashed figure in diagram), Joe is at a distance

               d(left)  = sqrt( [2m]^2 + [2.75m]^2 ) = 3.40 m

               d(right) = sqrt( [2m]^2 + [1.75m]^2 ) = 2.66 m

          So the difference in path length now is 

               d(left) - d(right) = 3.40 m - 2.66 m = 0.74 m

          Since the difference is exactly 1 wavelength, the two waves
          interfere constructively.

This page maintained by Michael Richmond. Last modified Feb 26, 1997.