Rotational Kinematics

Rotational Kinematics

The motion of objects as they translate -- move bodily from one place to another -- follows a simple set of rules. It turns out that a very similar set of rules describes the motion of objects as the rotate -- spin around in place.

Physicists usually don't use degrees as a unit to measure angles; instead, they use radians, which are ratios of the arc length described by an angle to the radius of the arc:

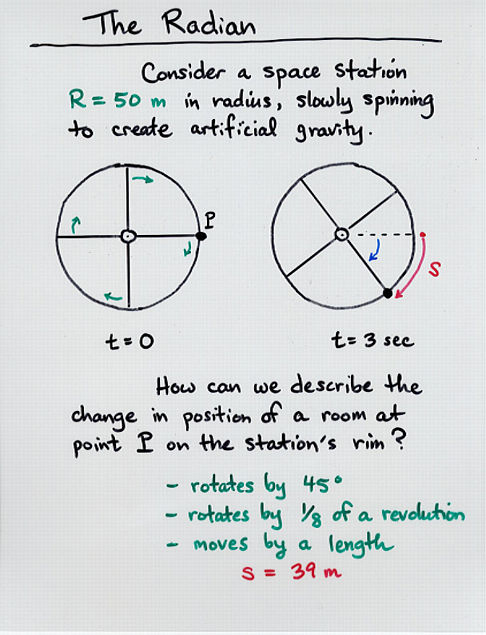
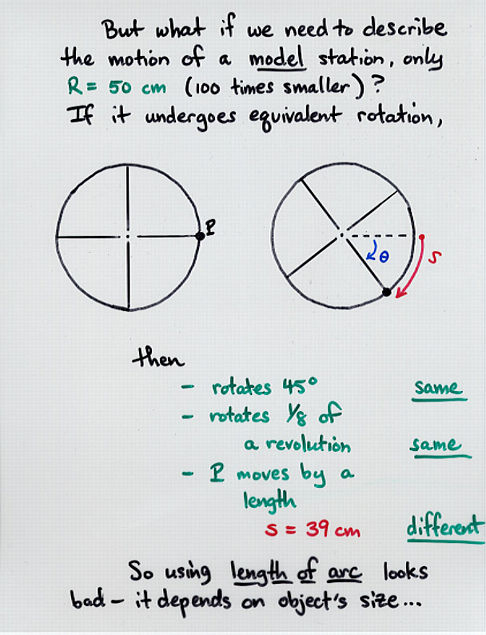
                               length of arc
          angle in radians =  ---------------
                                 radius

There are 2*pi = 6.28 radians in one full revolution. Therefore


                2 * pi radians =  360 degrees

                -->  1 radian  =   57.3 degrees

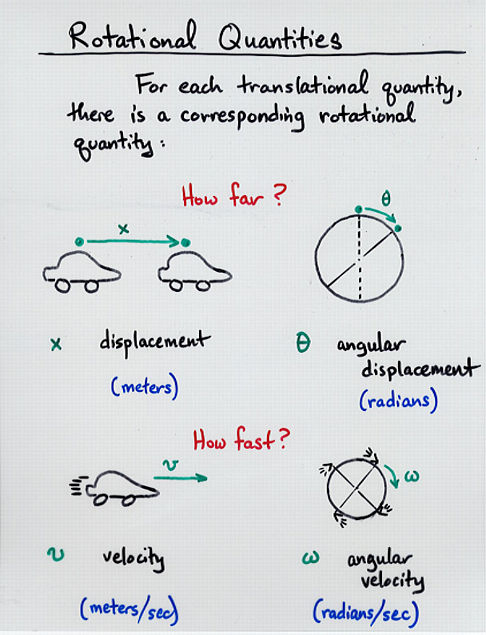
Each translational quantity has a rotational analog:

      displacement (meters)       -->     angular displacement (radians)

      velocity     (meter/sec)    -->     angular velocity (radian/sec)

      acceleration (meter/sec^2)  -->     angular acceleraion (radian/sec^2)

These rotational quantities obey a set of kinematic equations, exactly analogous to the 1-D translational kinematic equations.

Viewgraphs