The connection between SHM and waves

Let's pick a concrete example of simple harmonic motion (SHM). Suppose that you are in the back yard, next to a long, thin rope used to hang laundry; there's nothing hanging from it today. You see a bright red piece of fluff gently float through the air and land on the rope. As you watch, the rope wobbles a bit in the breeze, causing the red fluff to move up and down.

You check your watch and note that the fluff takes 62.8 seconds to complete 10 full cycles of motion.



  Q:  Can you write down an equation which describes
      the vertical position of the fluff as a function
      of time?



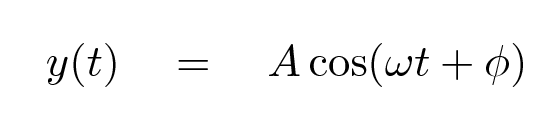
  Q:  What are the values and units of the quantities 

          A 

          ω 

          φ

That wasn't so hard. We can display this motion graphically by making a plot in which time runs along the horizontal axis and the position of the fluff is shown on the vertical axis, like this:

Look at the time between two successive peak positions of the fluff.



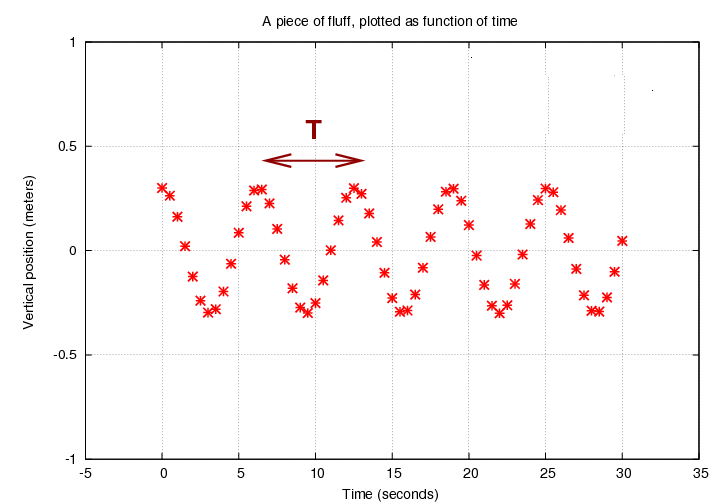
  Q:  What is the quantity T shown in this graph?


  Q:  How is it related to the angular frequency ω?

However, we can also, if we wish, pay attention to the OTHER PORTIONS of the rope, the sections on either side of the red piece of fluff. Suppose that we use a camera to take a picture of the rope around the fluff. It might look like this:



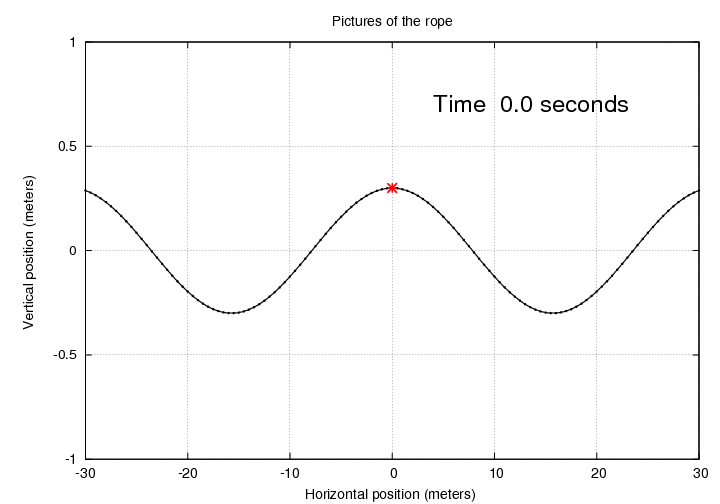
  Q:  Can you write down an equation which describes
      the vertical position of the rope as a function
      of POSITION (not time)?

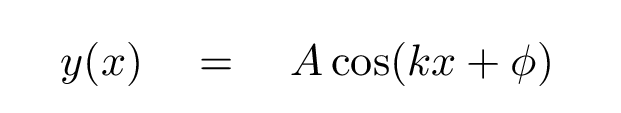
Look at the distance between two successive trough positions of the fluff.



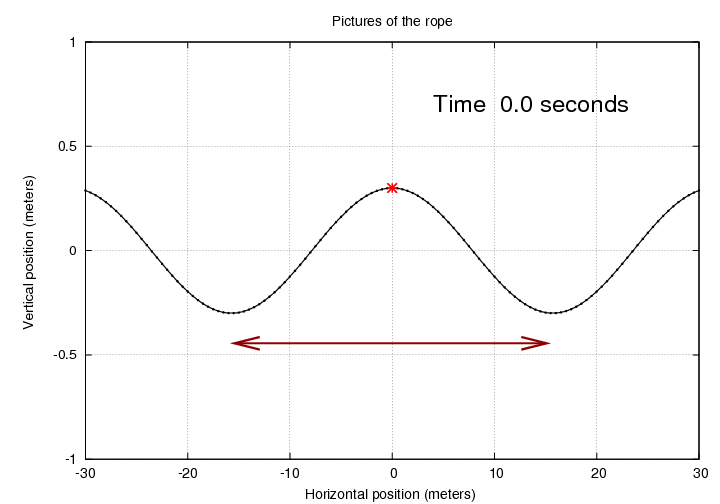
  Q:  What is the quantity shown in this graph?



  Q:  How is it related to the constant k in the equation above?

Hey, that looks pretty familiar. But this time, the argument of the cosine function isn't an angular frequency -- it's a spatial frequency. The quantity multiplied by the position is called the wave number k.


                                radians         2 π radians
    ω = angular frequency  =    -------     =   ---------
                                 second          period T 


                                radians         2 π radians
    k = wave number        =    -------     =   ----------
                                 meter          wavelength λ

Now, what happens if we watch the rope over a long stretch of space, and over a long stretch of time?



  Q:  Does the fluff move horizontally?


  Q:  Does any of the rope move horizontally?


  Q:  Does the pattern of the wave move horizontally?

Yes, in general, the PATTERN of a wave does move through space, even if the individual pieces of rope -- or air, or water -- are simply oscillating back and forth and not translating in any fixed direction over long periods of time.

Not all waves move in this fashion, but many do. Those which do move are called travelling waves,

How fast does the pattern move? It would be nice to express this speed in the standard units of meters per second. How can we do that?


                              radians
    We have         ω  =  -------------
                              second


                              radians
                    k  =  -------------
                              meter


    How can we combine these quantities to yield
    a speed?

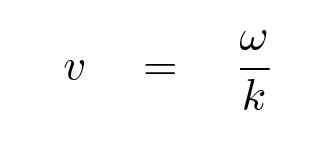
Right. So, putting everything together, we can write the equation for a travelling wave as a combination of an oscillation in time (good old SHM) and also in space:

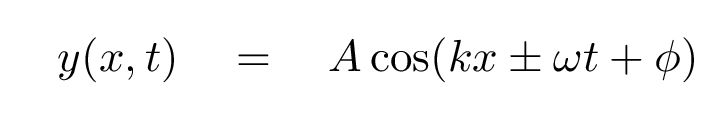
Which sign correponds to which direction?

But which sign, + or -, corresponds to a wave moving to the right?

One way to find out is good old trial-and-error. Let's plot some wave functions and see what happens. Use the Desmos calculator to execute the following commands:



    A = 1

    k = 1

    w = 1

    t = 0


    A * cos(k*x + w*t)

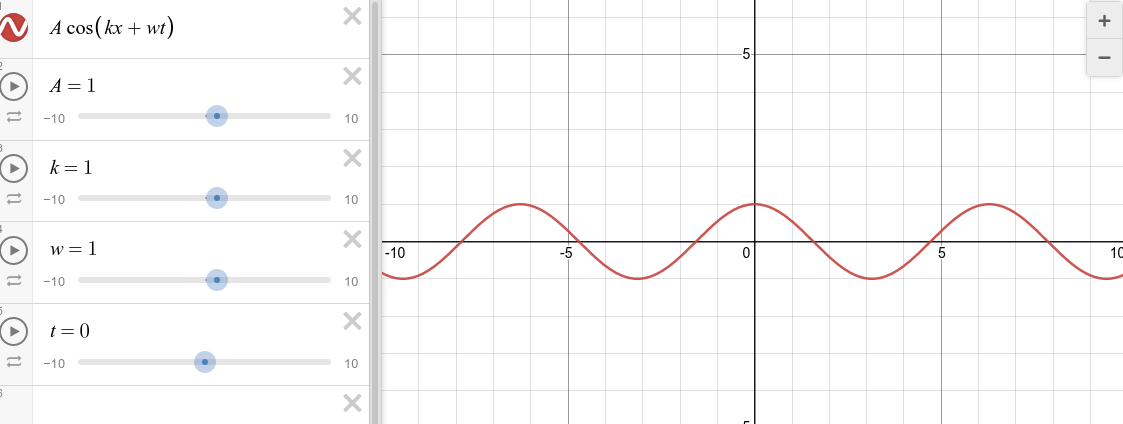
Graph made with the very nice Desmos on-line tool.

Concentrate on the peak of the function located at x = 0. Which way will that peak move if we allow time to march forward?

We can move time forward by moving the slider control next to the t variable to the right.

As we move the slider to the right, the value of the variable t increases ... and the graph changes to show the motion of the pattern with time.

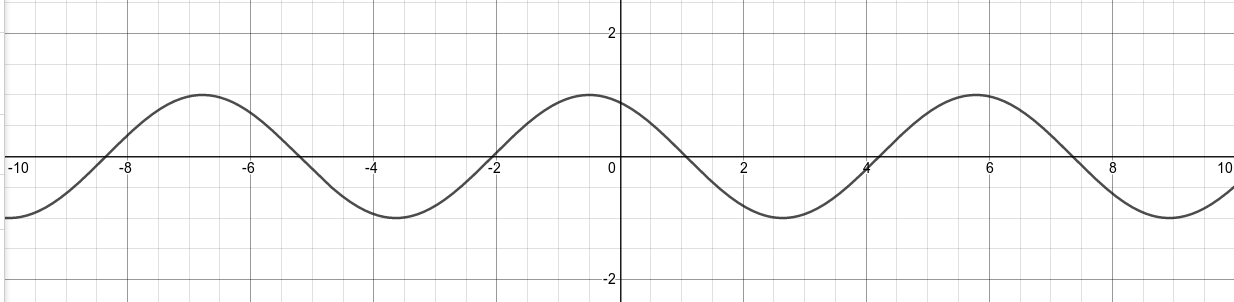
Graph made with the very nice Desmos on-line tool.

As you can see, given the equation



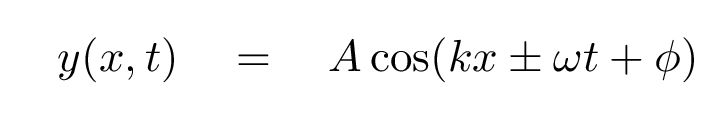
      if    (kx  +  ωt)         wave moves in NEGATIVE x direction

      if    (kx  -  ωt)         wave moves in POSITIVE x direction

One can also use mathematical reasoning to come to the same conclusion. The cosine function has a maximum value when its argument is zero: cos(θ) = 1 when θ = 0. But if θ = kx + ωt, then



      kx + ωt = 0          when       kx = -ωt

                                      so if  t > 0, then x < 0 


      kx - ωt = 0          when       kx = ωt

                                      so if  t > 0, then x > 0

The phase constant term φ also affects the location of the pattern. Please use Desmos -- or perhaps your calculator -- to answer the following questions.

Suppose that our wave has the equation

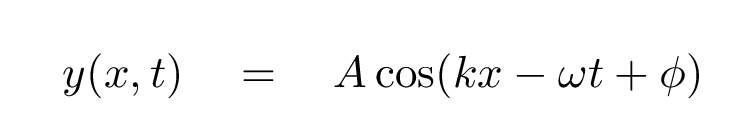
Look at the value of this wave around the position x = 0 and at time t = 0.



  Q1:  If we add a positive phase, φ = +0.5 rad, which direction
           does the pattern move?

             a) the pattern shifts in the POSITIVE x direction

             b) the pattern doesn't move at all

             c) the pattern shifts in the NEGATIVE x direction



  Bonus: How large must φ be in order to shift the
             pattern by exactly one wavelength?