Finding the uncertainty in the hypotenuse of a triangle

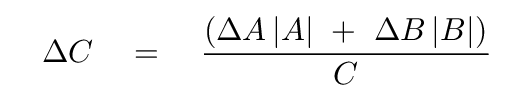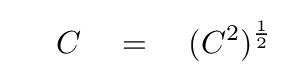
Pythagoras says that

              C2  =  [ A2  +  B2 ]

The uncertainties in A² and B² are

 
  (      ΔA     )            (      ΔB     )
  ( 2 * ------  ) * A2       ( 2 * ------  ) * B2
  (      A      )            (      B      )

which means that the uncertainty in C² must be the sum:

 
             (      ΔA     )            (      ΔB     )
 Δ(C2) =     ( 2 * ------  ) * A2   +   ( 2 * ------  ) * B2
             (      A      )            (      B      )

which simplifies to

 
 Δ(C2) =     ( 2 * ΔA * A   +   2 * ΔB * B ) 

Now we use the rule for propagating uncertainties when an expression is raised to the one-half power. Since the hypotenuse C is simply the square root of C²,

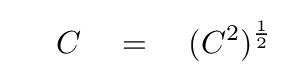
the rules say that the uncertainties in C and C² are related like so:

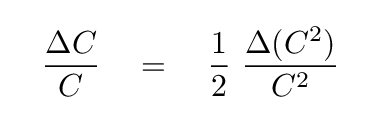
We can do a bit of algebra, and substitute our expression for the uncertainty in C² from above,

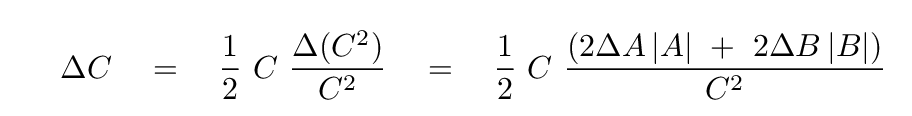
and the end result is not so complicated: