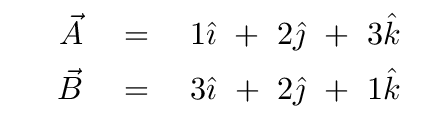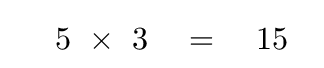
If someone hands us to scalars -- simple numbers, like 5 and 3 -- and says "multiply these!", there is no ambiguity. There's only one way to multiply two scalars.
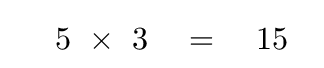
On the other hand, if we are told to multiply two VECTORS,
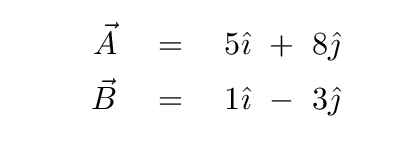
then there are two possibilities:
Q: What is the dot product of vectors A and B
shown above?
(Not sure what to do? Maybe this will help. )
Let's learn more about the cross product. It's a complicated subject, so let's take it a little at a time.
First, this product of two vectors always produces a vector which is perpendicular to the two inputs. So, for example, if we are given two vectors in the x-y plane,
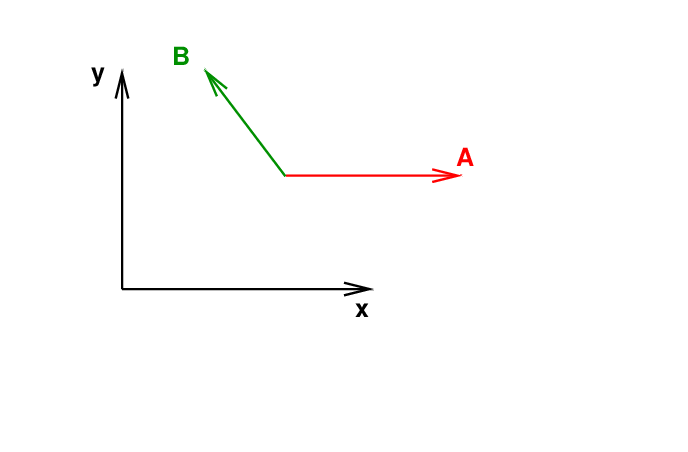
then their cross product must be in the +z or -z direction.
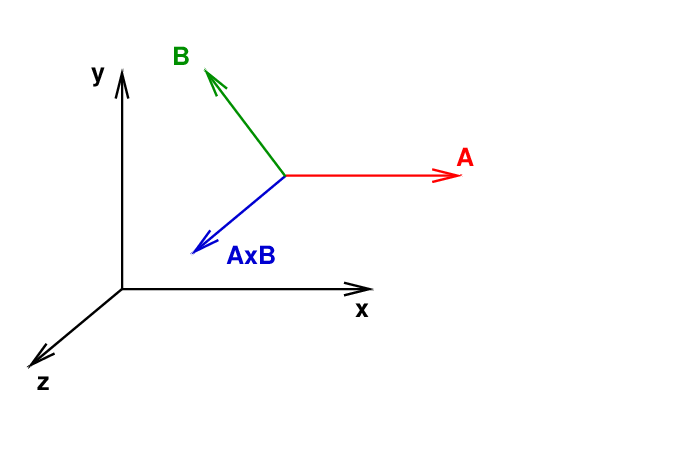
How do we decide between the +z and -z possibilities? The answer is -- surprise, surprise -- to use the right-hand rule.
So, in the example above, A × B points in the POSITIVE z direction.
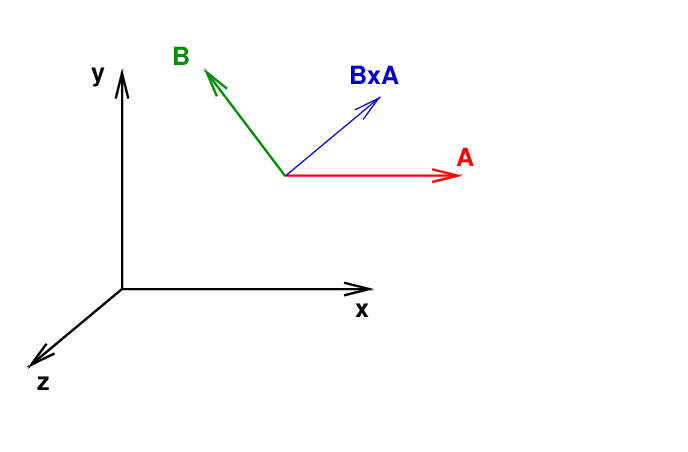
On the other hand, the cross product B × A produces a result in the NEGATIVE z direction.
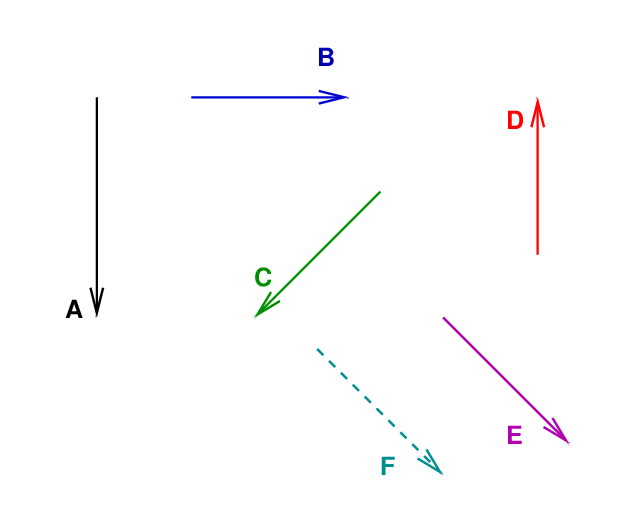
Let's practice. I'll pick two vectors, and you tell me the direction of their cross product.
Okay, that rule tells us the direction of the cross product. What about its magnitude?
Well, there are two ways to compute it. If you are given the angle θ between the two input vectors
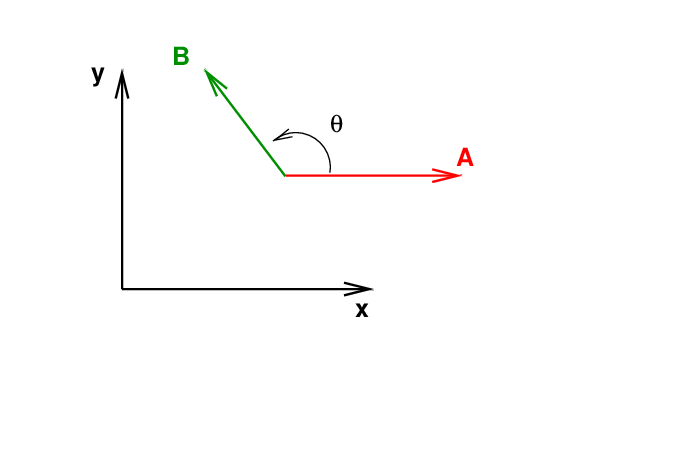
then the magnitude of the cross product is
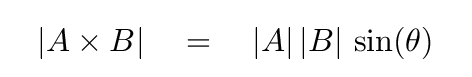
On the other hand, if you are given the input vectors in component form, like this,
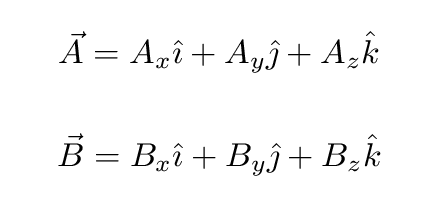
then you need to use some algebra. One can combine the components of the two vectors to form the cross product A x B like so:
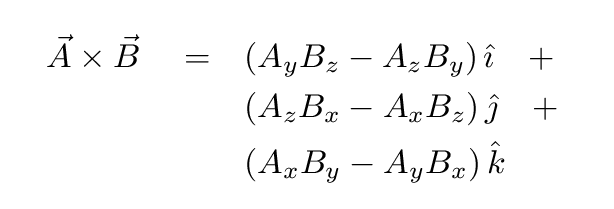
Let's try! Look again at the example we saw earlier:
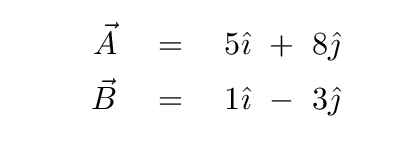
Q: What is the cross product of vectors A and B?
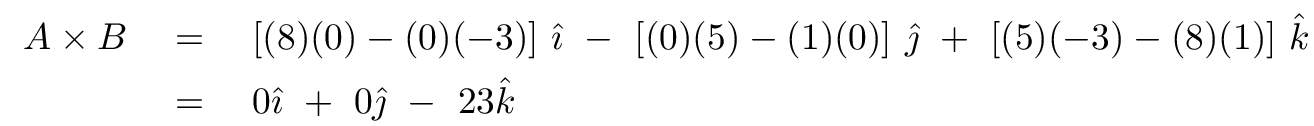
One way to remember this particular arrangement is to consider the cross product as a determinant:
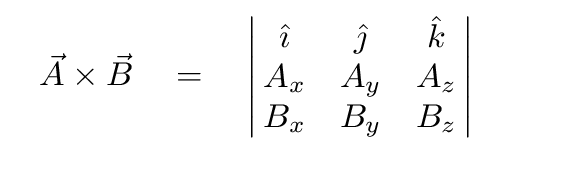
Now, when we compute the torque in a physics problem, we are interested in one particular cross product:
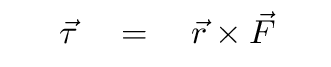
Note several things:
Given two vectors: