We have seen how to analyze the motion of a simple pendulum -- one which consists of a compact mass suspended from an ideal, massless string. But we can cause all sorts of objects to oscillate back and forth under the influence of gravity. How can we understand the motion of these non-simple, or "physical", pendula?
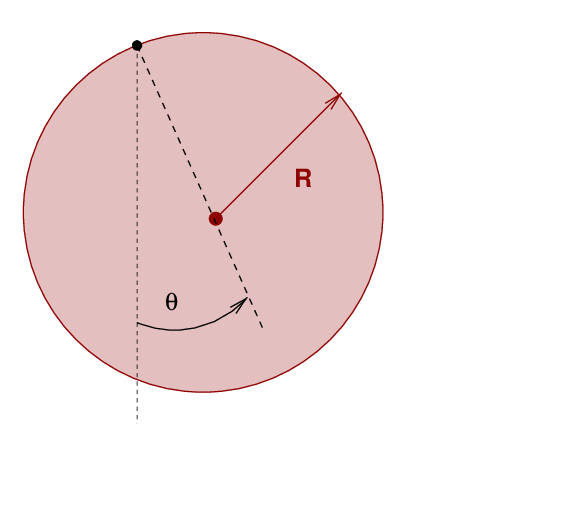
Suppose that an object of mass m, is suspended from some pivot point, P. In this example, I'll choose a disk of radius R.
At rest, the object hangs vertically down from the pivot, with its center of mass directly under P. We displace the object from its vertical orientation by an angular displacement θ, then release it.

Q: What are the forces acting on the object?
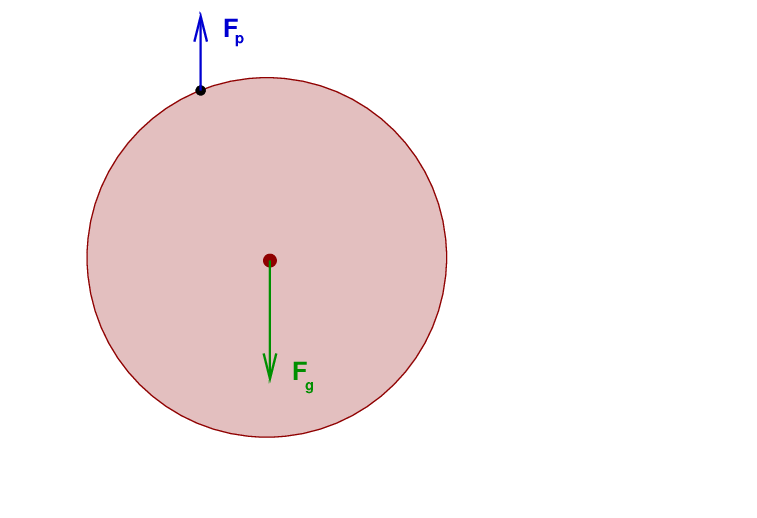
Okay, so there are two forces. We know the object will swing around the pivot, so let's compute the torque around this point due to each force.
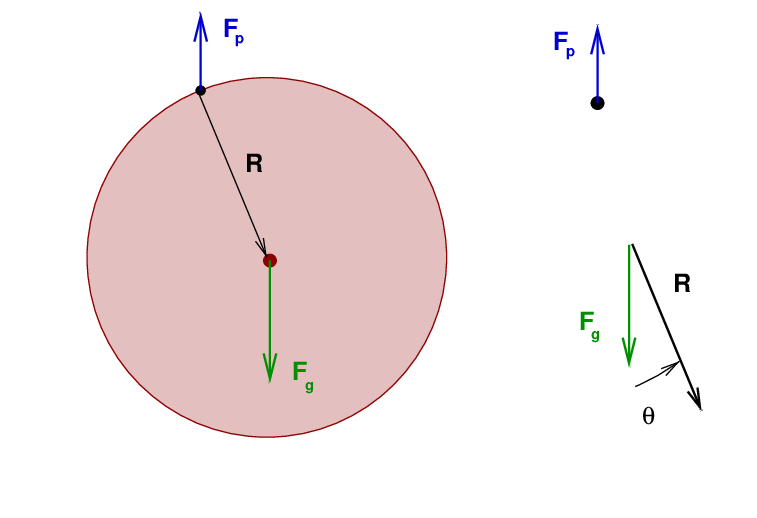
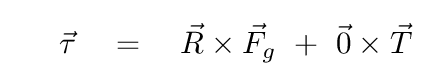
The force of the pivot is a distance of ZERO away from the pivot, so its torque must be zero. That leaves only the torque due to gravity ... which we can simplify for small angles.
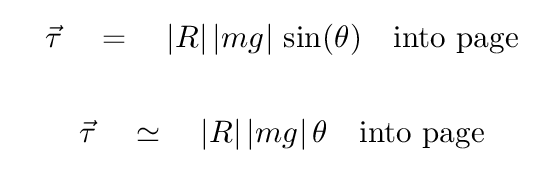
As we saw before, the angular displacement (OUT of the page) is opposite to the direction of the torque (INTO the page). Since the two vectors point in opposite directions, we can write
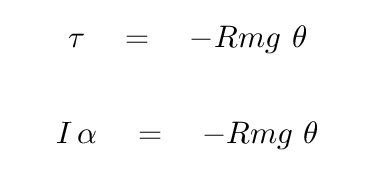
Now, the big question with a physical pendulum is the moment of inertia.
Q: What is the moment of inertia of the object around the pivot?
Right.
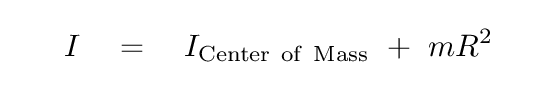
Therefore,
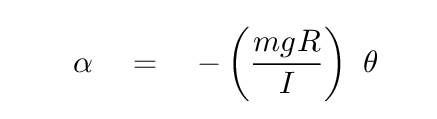
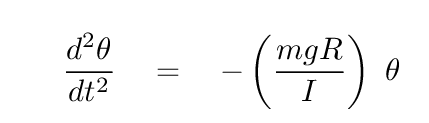
That's a differential equation that we've seen before. We know how to solve it -- the solution will involve sines or cosines. To make the result look nicer, let's define a variable
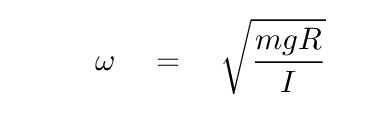
so that we can write the differential equation as
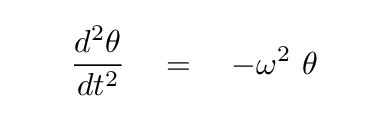
And you know how to take things from here.