Results of the Swinging Ring Experiment (spring 2026)

The goal of this experiment was to predict the time it takes a small metal ring to swing back and forth. Students made measurements of the oscillations of a set of large rings, and tried to find some mathematical way to extrapolate to the behavior of a small ring.

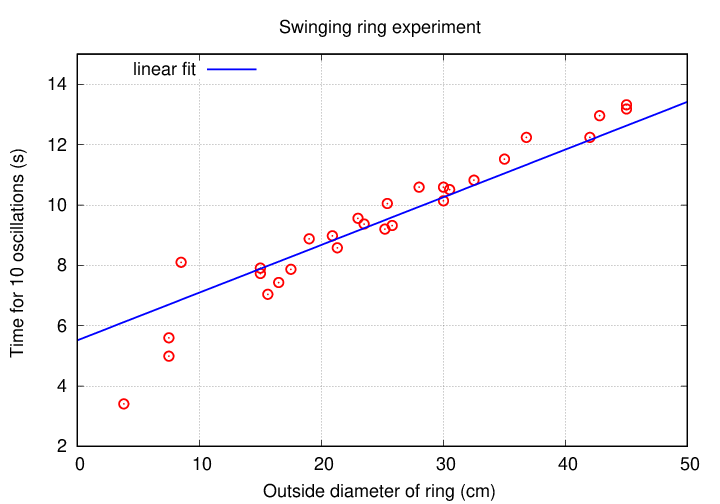
Here are the collected measurements made by all the groups in class: Note that a simple linear fit doesn't do a very good job.

There was one measurement of the 8.5-cm ring which appeared to be an outlier. If we remove that value from the data and make another linear fit, it's not bad ...

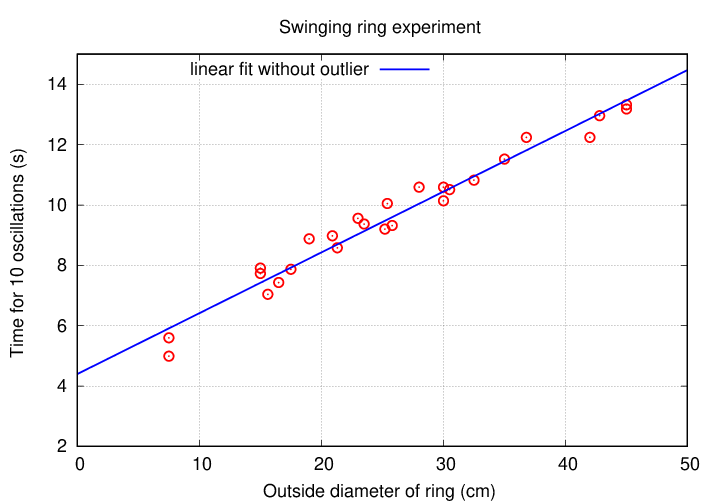
... but note that there's a pattern:

measurements of time for the smallest rings lie BELOW the fit
measurements of time for the middle-sized rings lie ABOVE the fit
measurements of time for the largest rings lie BELOW the fit

Based on similar linear fits to the data, students predicted the time for 10 oscillations of a tiny ring of diameter d = 3.8 cm. Some of the predictions were (all times in seconds)


    4.20  5.14  5.15  5.25  5.46  5.54  5.87  5.87  5.87

It turns out that all of these predictions are TOO LARGE. Hmmm. There seems to be a problem with the model of a linear relationship between period and diameter of the ring.

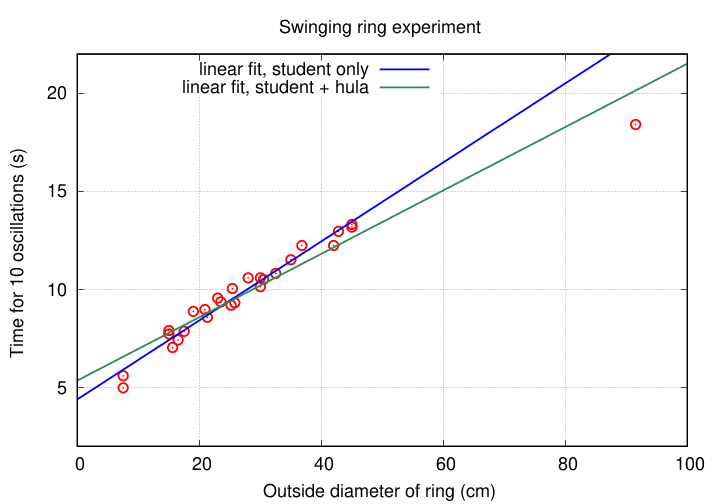
Before our class met, I measured the oscillations of a much larger ring: a hula hoop. If we add those measurements to the dataset, one can see more clearly that a simple linear fit to (time vs. diameter) doesn't work well.

That means that the period does NOT follow a relationship like

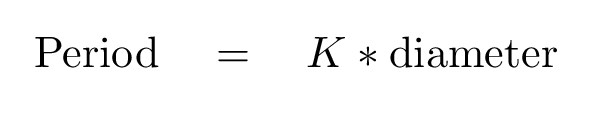
On the other hand, if we compute the LOGARITHM of each quantity, and plot log(time for 10 oscillations) vs. log(diameter), then we see a pretty nice linear relationship:

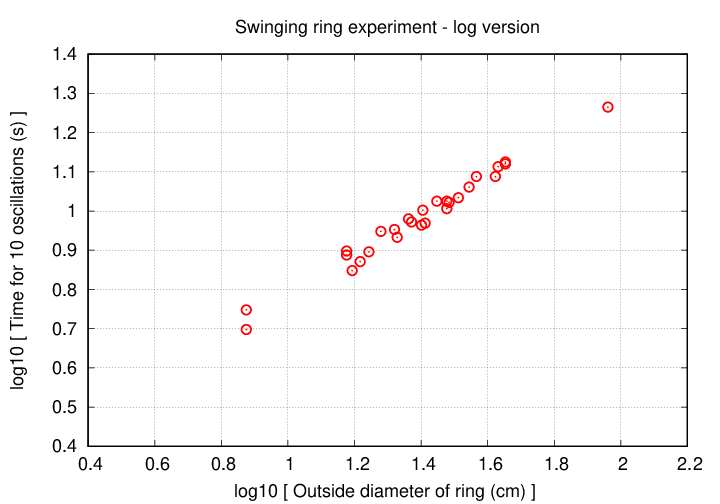
I'll hand out copies of this log-log version of the graph. Your will have three tasks:

measure the slope of a linear fit to this data
measure the UNCERTAINTY in the slope
predict the time for 10 oscillations of the tiny ring. Note d = 3.8 cm means that log₁₀(d) = 0.58.

Some hints on finding the uncertainties in a slope

You should find that the slope of this relationship is just about 0.5.

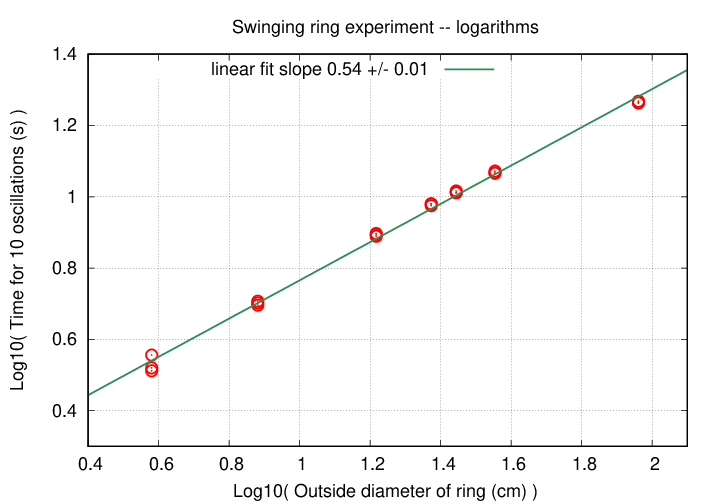
That means that we could write



        time to oscillate  =  K * (ring diameter)^0.5

        time to oscillate  =  K * sqrt( ring diameter )

And, in fact, fitting the data to a square-root relationship works very nicely.

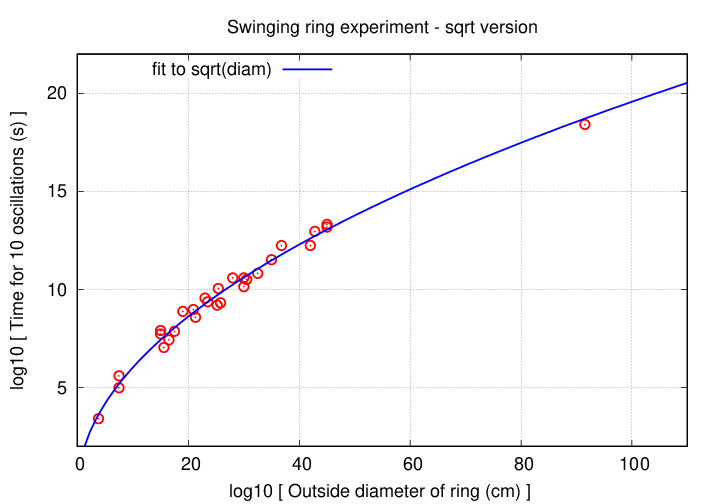
Extrapolating the line to a ring which has diameter 3.8 cm, so at an x-value of log10(3.8) = 0.58, yields a time for 10 oscillations of t = 3.4 seconds.