 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Regular old linear momentum can help one to solve problems involving collisions of objects moving in straight lines, but angular momentum is the tool to use when objects are constrained to swing or move in circular paths.
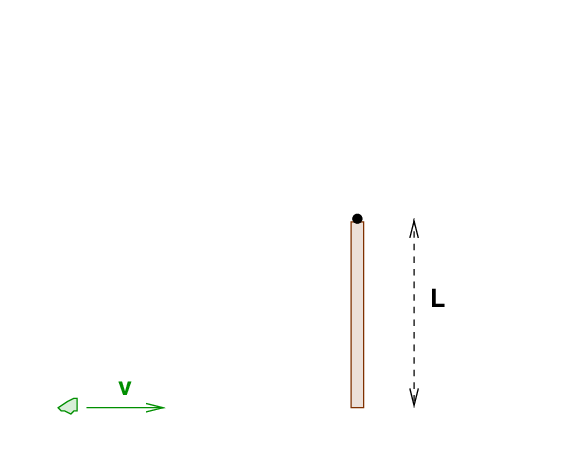
Consider a long, thin rod of mass M = 2.0 kg and length L = 1.2 m which lies on the icy, frictionless surface of a frozen pond. One end of the rod is attached to a pin stuck in the ice, so that the rod can swing freely around the pin.

A small wad of putty, of mass m = 0.4 kg, slides across the ice at with speed v = 6.0 m/s.
Q: What is the angular momentum of the rod
around the pin, before the collision?
Q: What is the angular momentum of the putty
around the pin, before the collision?
Q: What is the total angular momentum of the
system around the pin, before the collision?
When it reaches the rod, it sticks to the very end, causing it and the rod to start swinging counter-clockwise.
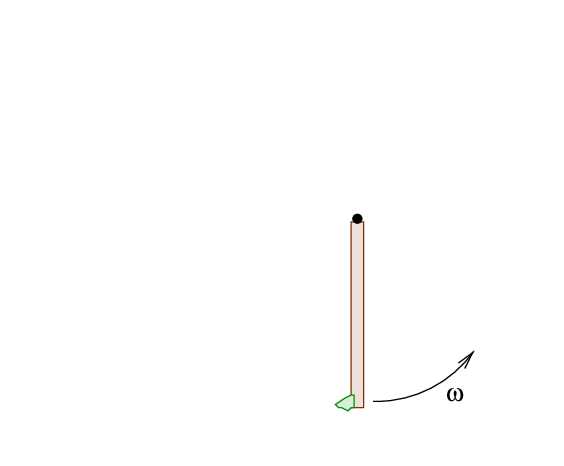
One can use conservation of angular momentum to figure out the angular velocity of the rod-plus-putty combination.
Q: What is the moment of inertia of the rod-plus-putty
around the pivot?
Q: What is the angular velocity of the rod-plus-putty object?
Now, the rod-plus-putty continues to swing around the pin. As it moves, another wad of putty -- identical to the first in mass -- slides toward the rod at speed u. This second wad will strike the rod at a distance L/2 from the pin.
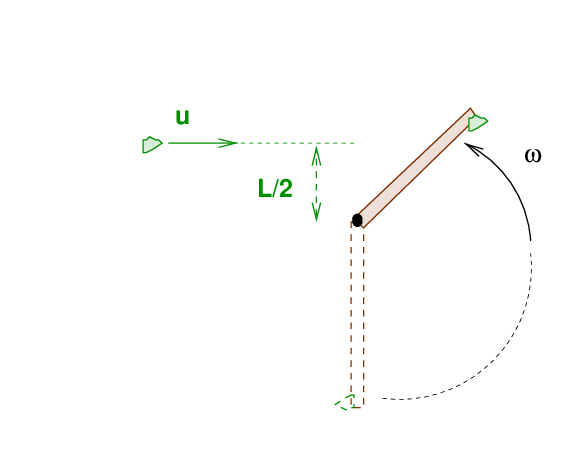
Just as the rod swings through exactly 180 degrees, the second wad of putty runs into it, and sticks to it. Amazingly, the speed of the putty was just right to cause the rod (now with two wads of putty) to stop completely.
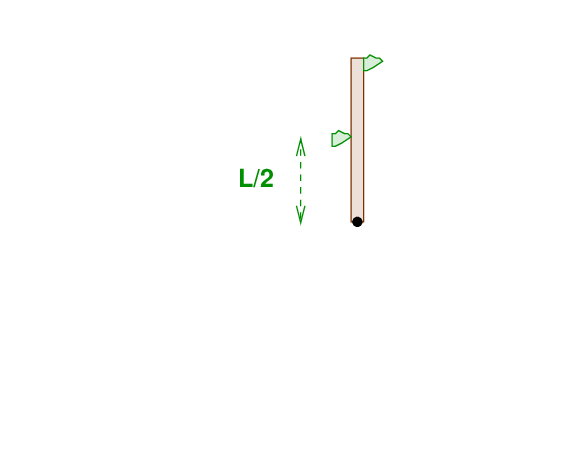
Q: What speed u will cause the rod to come
to a complete stop?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.