 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
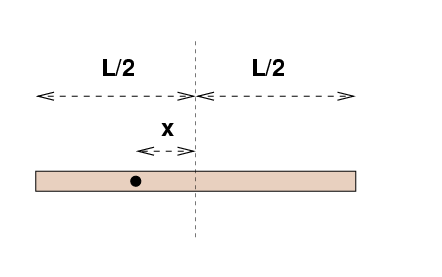
Let's create a sort of pendulum by drilling a hole a distance x from the center of a meterstick.

We can suspend the meterstick from a pin through this hole, and then nudge the meterstick so that it rotates around the pin.
The meterstick has a mass M and length L (which should be 1 meter, of course). What's the moment of inertia of the meterstick around this hole?
Right.
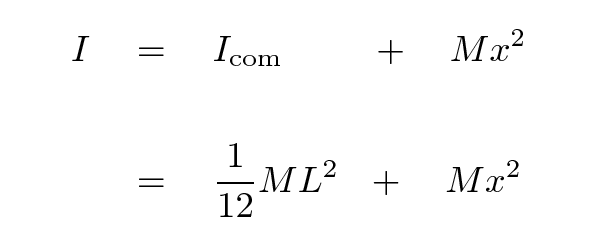
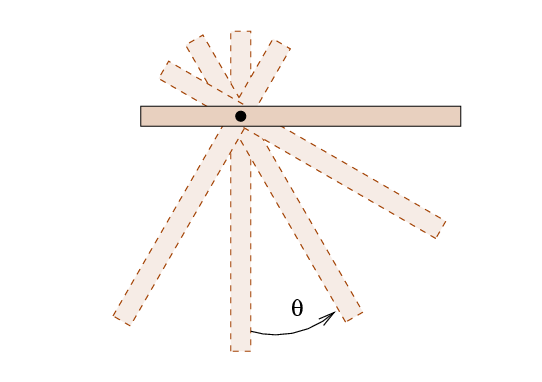
Okay, now, if we let the meterstick hang straight down for a moment, and then displace it by a small angle θ as shown below, gravity will exert a torque on the stick. The cross in the picture marks the location of the center of mass of the meterstick.
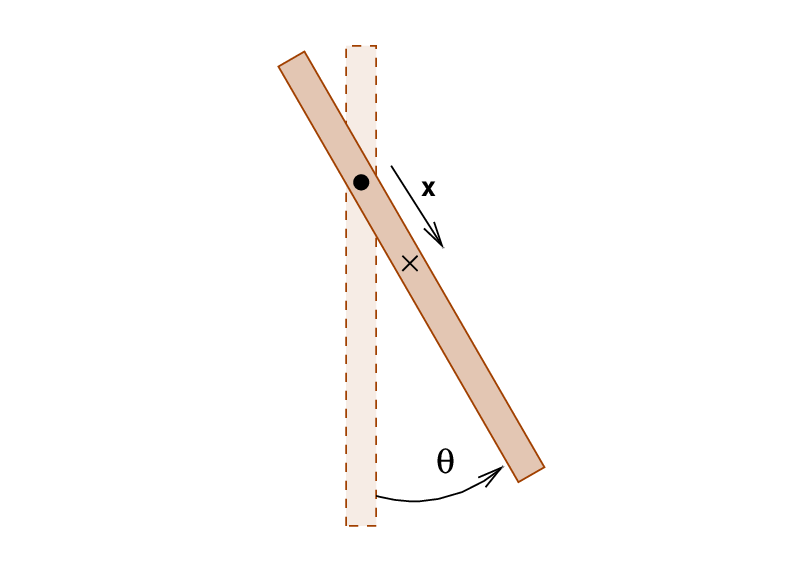
Q: What is the torque on the meterstick around the pivot?
The magnitude of the torque will be
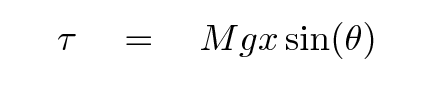
Q: What's the direction of the displacement θ? Q: What's the direction of the torque τ?
Okay, so we know the torque and the moment of inertia. When we release the meterstick, it will start to rotate.
Q: What is the angular acceleration of the stick?
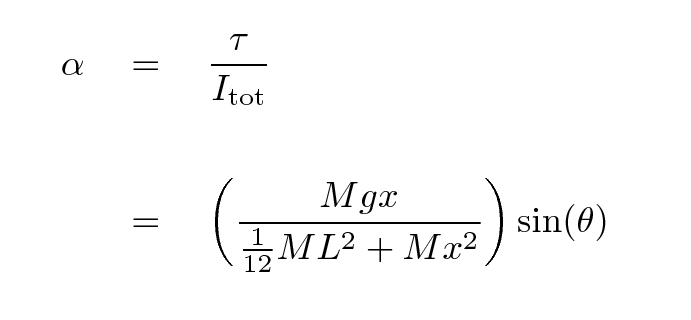
Q: What's the direction of the angular acceleration α?
Now, as we saw last week, it turns out that if the angle θ is small -- say, 10 degrees or 15 degrees, then expressed in radians
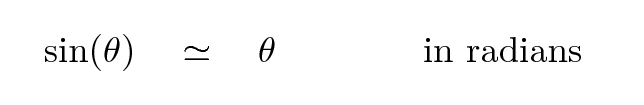
Putting all this together, we can now say that the meterstick will accelerate like so:
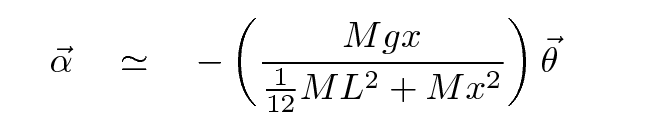
Q: Hey! Isn't the angular acceleration related
to the angular displacement?
Why, yes, it is. In fact, it's the second derivative of angular displacement with respect to time,
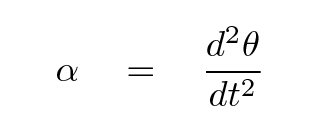
So, putting everything together, this means that the motion of the meterstick -- as long as the angular displacements are small -- will follow the differential equation
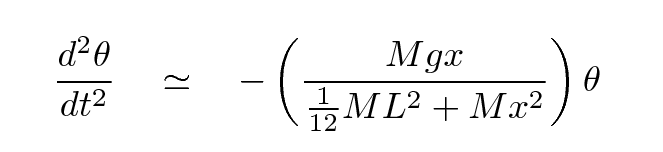
Q: Can you write an equation which shows how
the angular displacement θ
will change with time?
Q: Suppose that the offset between the
center of the meterstick and the hole is
x = 0.2 m.
What is the equation now, with numbers?
Q: What will the period of the meterstick be?
If we have time, perhaps we could investigate these questions.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.