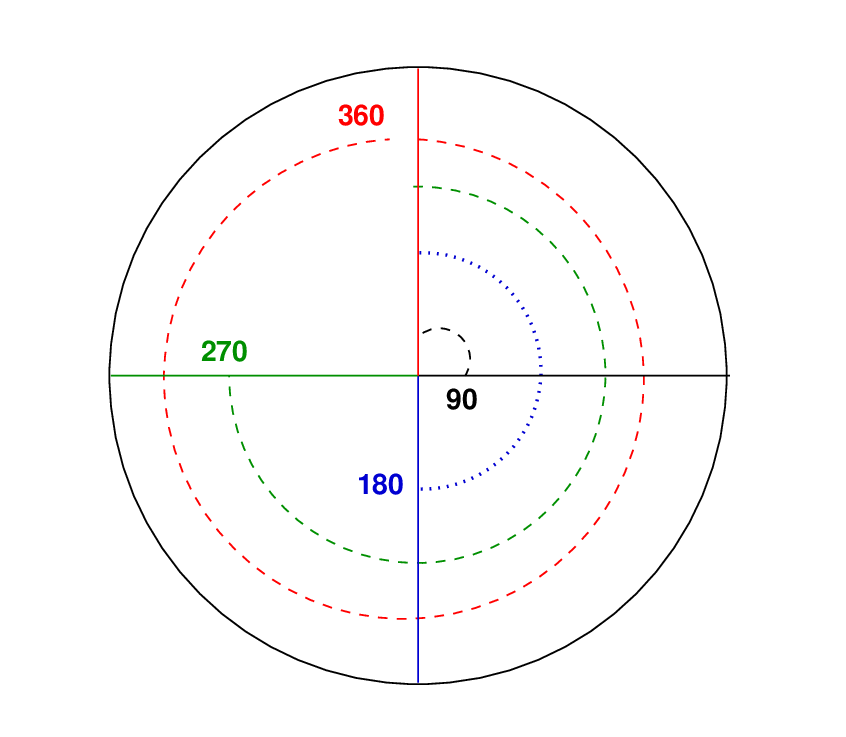
When you started learning about geometry and circles and other shapes, you probably learned about our usual method for measuring angles: degrees. By definition, there are exactly 360 degrees around one full circle.

Why 360? The choice was made thousands of years ago, and has three good reasons behind it.
Starting some five or six centuries ago, mathematicians began to discuss a different way to measure angles, one that was based on the properties of a circle itself. As we will see, this choice makes a number of mathematical operations easier to perform. Perhaps the first to suggest the adoption of this new measure was Roger Cotes, in the early eighteenth century. However, the name radian was not applied to this new unit until around 1873.
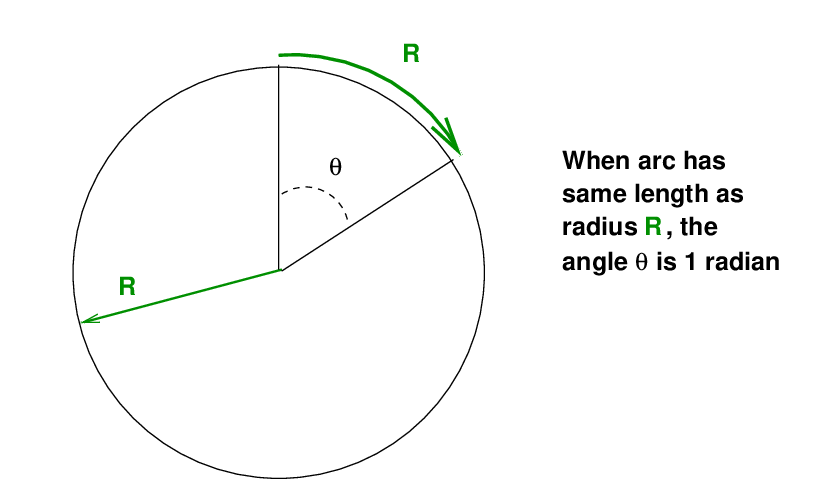
The radian is defined as the angle which produces a circular arc which has the same length as the radius of the circle.
That means that one entire journey around a circle corresponds to 2 π = 6.2832... radians.
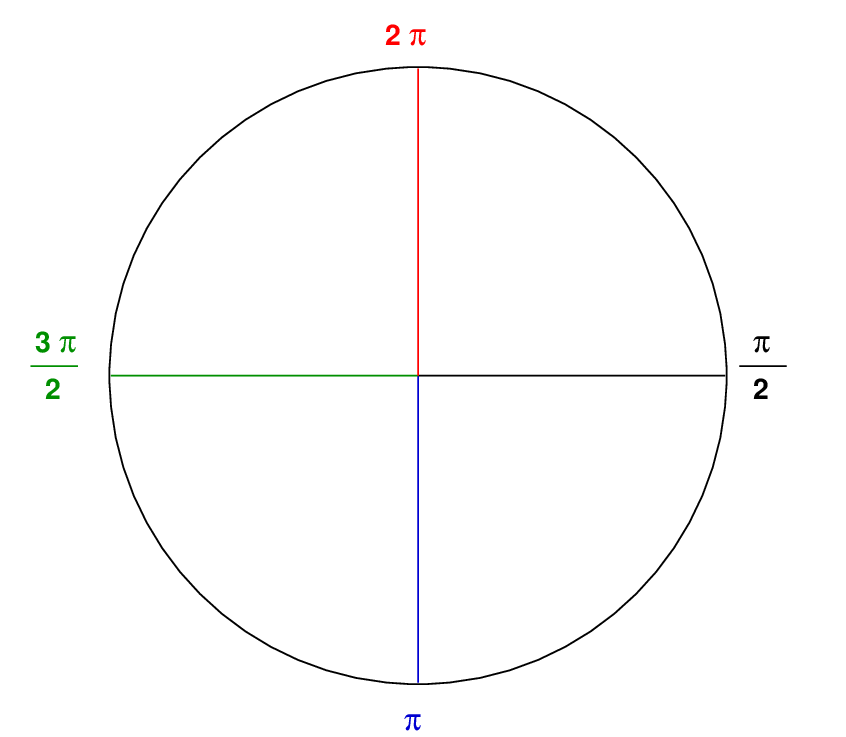
The Bad News about radians is that expressing ordinary angles requires either fractions, or decimals, or both; and nearly all these values correspond to irrational, if not transcendental, numbers.
The Good News is that calculations of the physical properties of rotating systems will be much, much easier if we express their properties in radians.