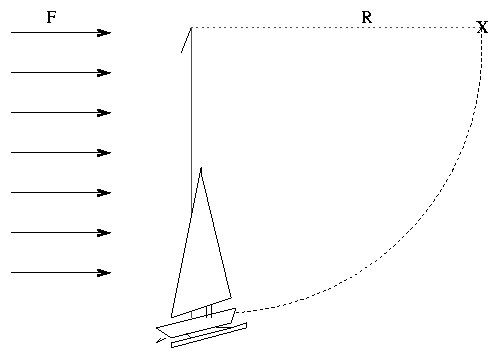
An iceboat of mass M = 250 kg sits motionless on a frozen lake. The boat is tied to a stake by a rope of length R = 100 m. A steady wind starts to blow from the West, pushing the boat with a constant force F = 150 N. The boat slides without friction along the ice, moving in a circular arc as the rope stretches taut.

How fast is the boat moving when it reaches the point marked "X"?

Please try to do this problem by breaking the motion of the boat along the arc into a number of little steps; assume that each little step is a short, straight line.

• draw a picture of the boat when the rope has swung through some angle θ from its starting position
• determine the angle between the force of the wind, and the direction of the boat's motion at this point
• figure out the work done by the wind as the boat moves by a little step in this direction
• your expression probably has two variables in it now: dx and θ. It will help to get rid of one of them, so that the work is a function of just one variable. Find a way to replace dx by some expression which has a dθ
• the expression for work done as the boat moves a tiny distance should include a sine or cosine of the angle θ, as well as a factor of dθ
• integrate the work as the boat moves from θ = 0 to θ = pi/2 .