 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
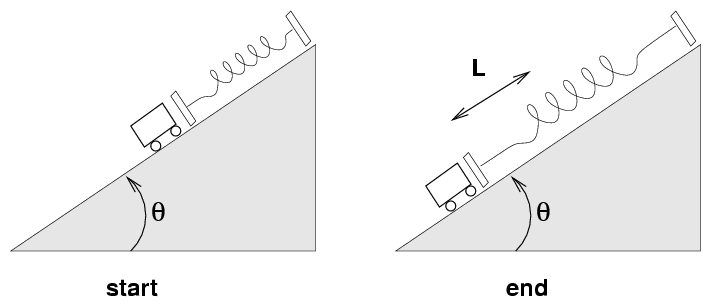
We place a cart of mass M on a ramp tilted at angle θ. It is attached to a spring of force constant k, which is initially at its rest length.

We hold the cart in the "start" position for a moment, then release it. The cart rolls down the ramp a distance L before coming to a momentary halt. It then starts back up the ramp, pulled by the spring. Ignore friction for the moment ...
Okay, now let's add friction. Suppose that the coefficient of kinetic friction between track and cart is μ.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.