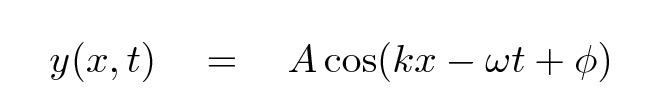
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
So, consider a tranverse travelling wave. Let's say that it is moving in the x-direction, and the displacement of its medium as it travels is perpendicular to that motion: in the y-direction. We can describe the position of particles in the medium in the following manner:
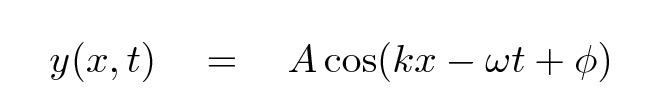
As time passes, the position of particles will change. They will oscillate up-and-down as the wave passes. Is there some way to figure out how fast the particles will move?
Q: How fast will the particles move in the tranverse direction?
Yes, there is a way. Since we know the y-position as a function of time, we can simply take the derivative with respect to time to find the y-velocity as a function of time:
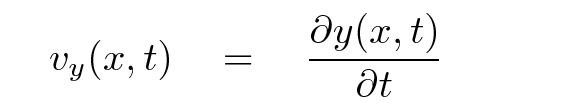
Q: Write an equation for vy as a function of space and time.
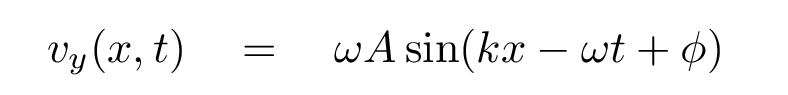
Fine.
But we don't have to stop there. We can take things one step further.
Q: Is there a way to figure out the tranverse acceleration
of particles in the medium?
Yup. Since we know the y-velocity as a function of time, we can simply take the derivative with respect to time to find the y-acceleration as a function of time:
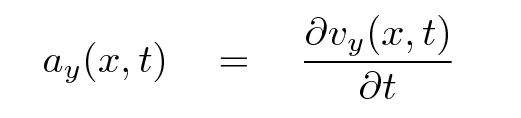
Q: Write an equation for ay as a function of space and time.
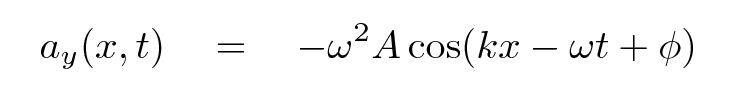
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.