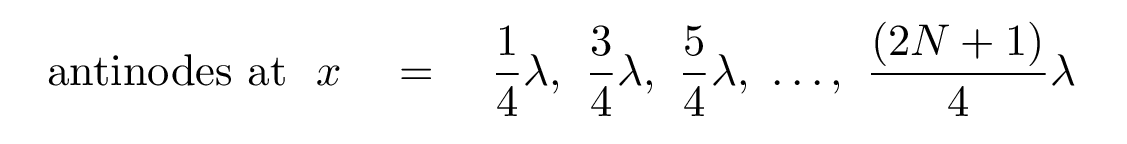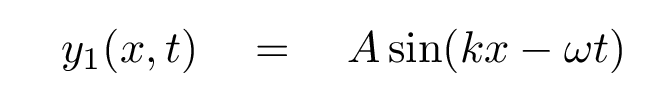
You know that we can describe a travelling wave with a mathematical form like this:
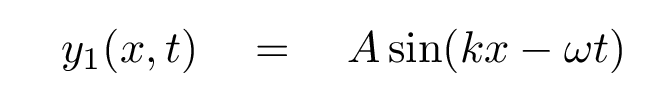
The equation above represents a wave travelling to which direction?
Q: The wave travels which way?
RIGHT LEFT
So an identical wave travelling in the OTHER direction will have an equation like this:
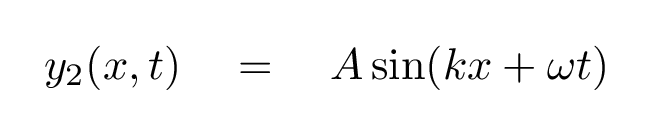
What happens when these two waves meet? Is there some way to add them together? Perhaps you might remember this little trigonometric identity ...
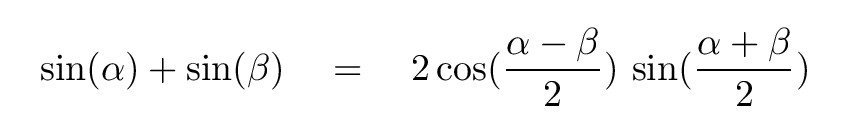
Q: Use the trig identity to add together the two waves
y1(x, t) and y2(x, t).
The result should simplify quite a bit.
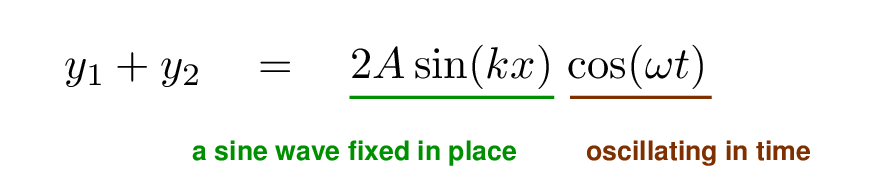
When two identical waves meet, travelling in opposite directions, they add up in a special way. The summed waves appears to stand still; the pattern doesn't slide to the right or the left. We therefore call it a standing wave.
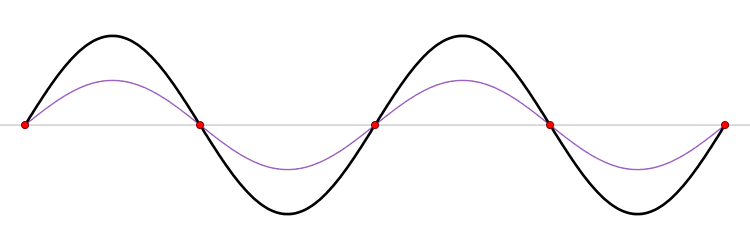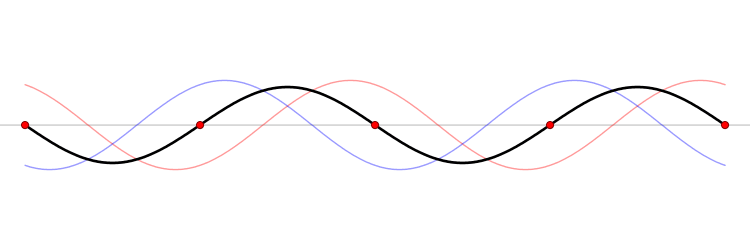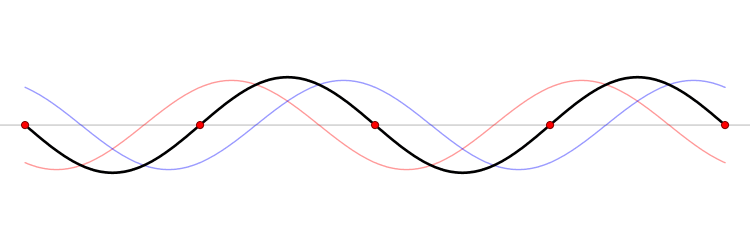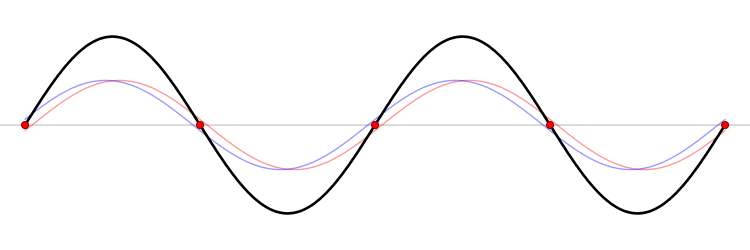
Image courtesy of
LucasVB and
wikimedia.org.
If you look at a standing wave
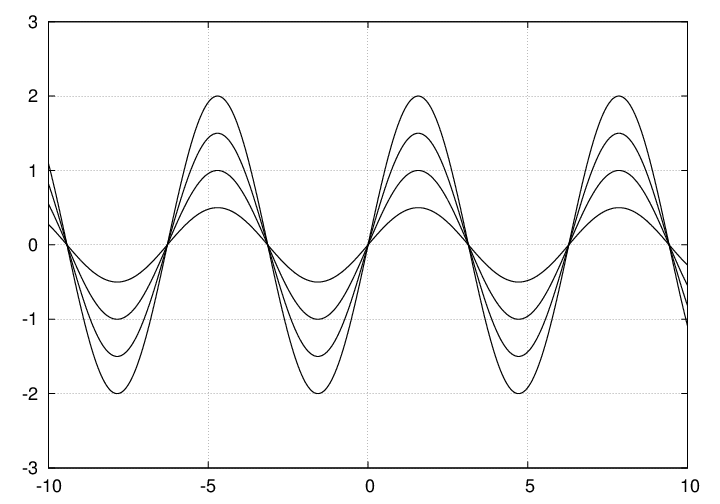
you can see that there are some locations at which the displacement is always zero. We call these locations nodes.
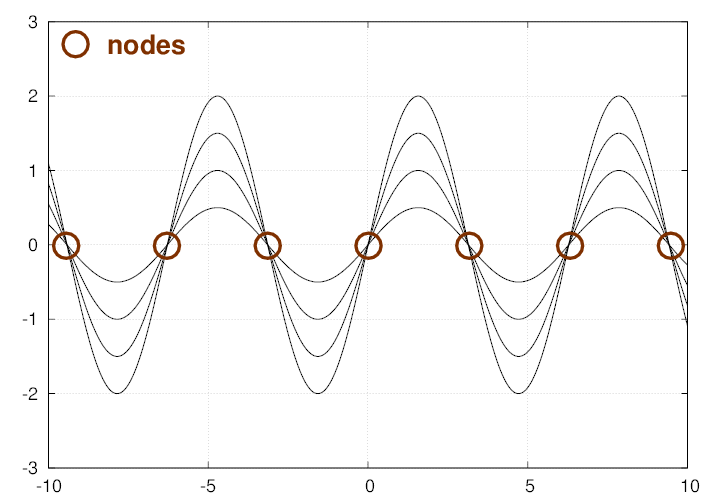
These nodes must occur whenever the position satisfies a particular condition:
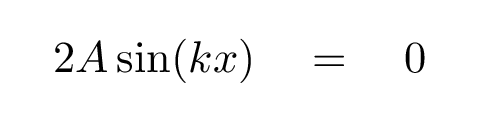
Q: When does sin(kx) = 0? Q: At what values of x will we find a node?
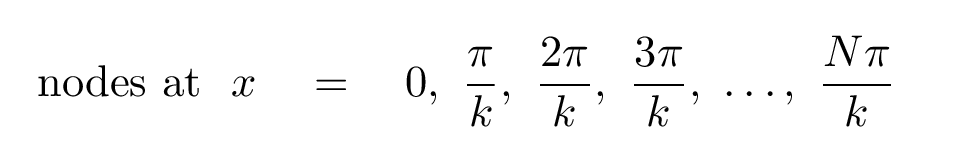
Right.
Hey, wait a minute. The wave number k is related to the wavelength λ, right? So we should be able to express the locations of nodes in terms of the wavelength, too.
Q: How is the wavelength λ related to wave number k? Q: Write the locations of nodes in terms of wavelength.
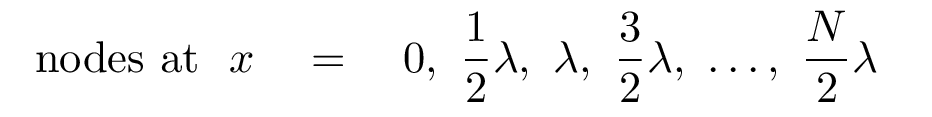
Let's look again at a standing wave:

This time, focus on the places where the displacement reaches a maximum value. We call these locations antinodes.
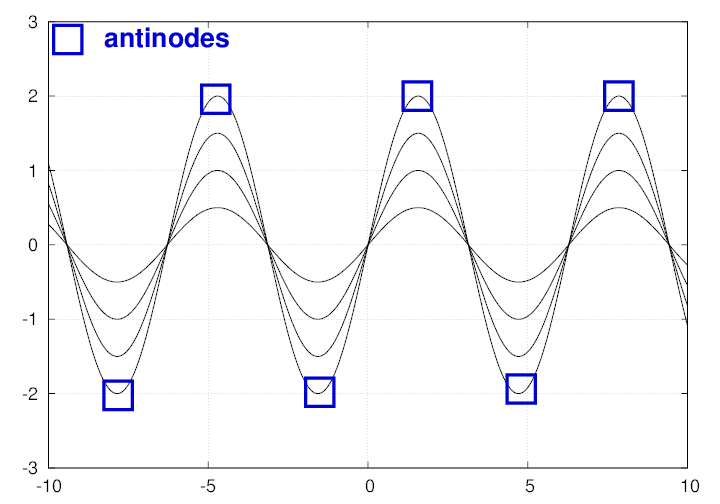
These nodes must occur whenever the position satisfies a different particular condition:
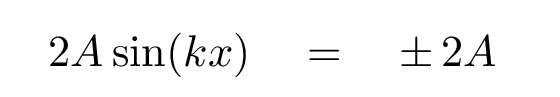
Q: When does sin(kx) = +/- 1? Q: At what values of x will we find an antinode?
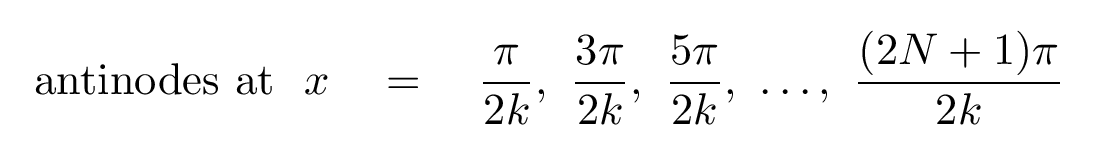
Right.
Hey, wait a minute. The wave number k is related to the wavelength λ, right? So we should be able to express the locations of antinodes in terms of the wavelength, too.
Q: Write the locations of antinodes in terms of wavelength.