Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
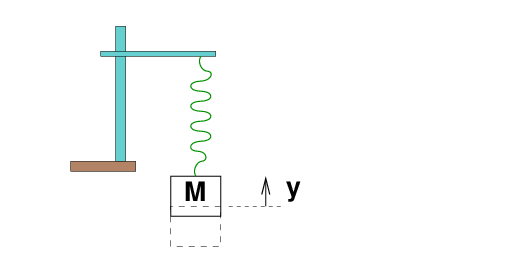
Suppose that a block of mass M = 2 kg hangs from a spring of force constant k = 20 N/m. The block is at rest, motionless.
You then raise the block a distance y = 0.1 m vertically, and release it. The block starts to bob up and down, up and down.
Q: Can you write an equation which describes the
position of the block as a function of time?
Right. It looks like this:
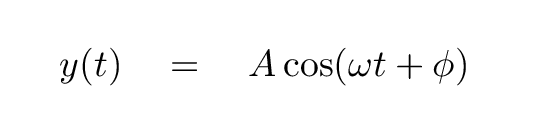
Q: In this particular case, what is the value of the
amplitude A?
Q: In this particular case, what is the value of the
angular frequency ω?
But that only tells us the position of the block. What if we want to know how fast the block is moving at any time -- the velocity of the block?
Q: Is there some way to write down the velocity as
a simple function of time?
Indeed there is: take the derivative of position with respect to time.
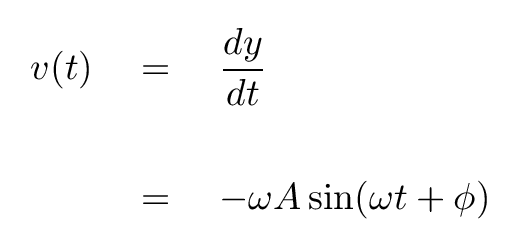
Q: In this particular case, what is the maximum
speed of the block?
In a similar manner, we can compute the acceleration of the block at any time by taking the time derivative of the velocity:
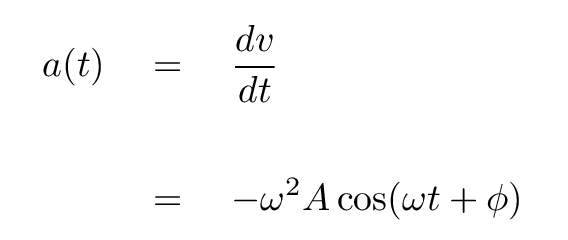
Q: In this particular case, what is the maximum
acceleration of the block?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.