Some SHM problems

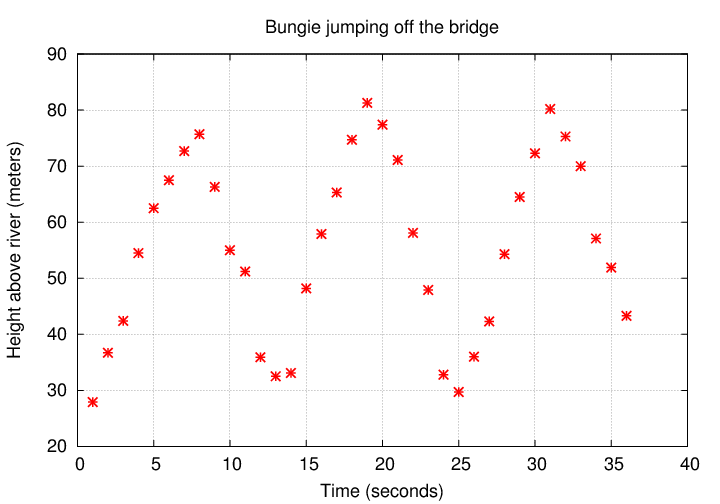
Crazy Ellie goes bungie jumping of the downtown bridge. Her friend Joe measures her position as she bobs up and down in the aftermath of one particular jump. in this data file .
1. What is the amplitude of the changes in height?
2. What is the period of the changes in height?
3. What is the angular frequency of the changes in height?
4. Can you write an equation which yields height H, in meters, as a function of time, in seconds, since the start of the data?
```
   
```
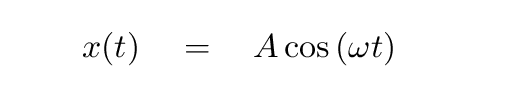
A block of M = 5 kg sits on a frictionless floor, connected to a spring of force constant k = 100 N/m. The other end of the spring sticks into the wall. I place the block at the spring's rest position. Then, I pull it an extra distance x = 0.1 m from the wall and let go at t = 0 s. The block slides left and right, left and right, so that its position at time t is given by
1. What is A in the equation above?
2. What is ω in the equation above?
3. What is the period of oscillation?
4. What is the maximum speed of the block?
I stop the block and again place it at the rest position of the spring. Then I pull it a larger distance from the wall, x = 0.2 m, and release it.
1. What is the period of oscillation now?
2. What is the maximum speed of the block now?
I hang a meterstick of mass m = 150 g by a hole which is h = 40 cm from the center of the rod. The meterstick is hanging straight down towards the floor, motionless.
1. What is the moment of inertia of the rod around this hole?
2. What is the force of gravity on the rod?
3. What is the torque on the meterstick?
4. Write an equation which shows the angular acceleration of the meterstick.
5. Write an equation which shows the angular acceleration of the meterstick as a function of the angular displacement.
6. Does the meterstick undergo simple harmonic motion? Explain.
7. What is the period of the meterstick's oscillation?