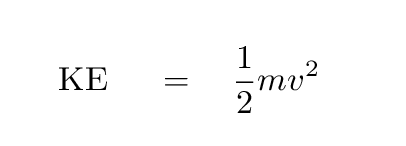
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You have probably discussed kinetic energy in an earlier physics course. Kinetic energy, or KE for short, is just one of many different types of energy.
Q: Can you name any other types of energy?
Try to be specific.
Kinetic energy is the energy a body has due to its motion. The formula for calculating the kinetic energy of a body (in the non-relativistic regime) is pretty simple:
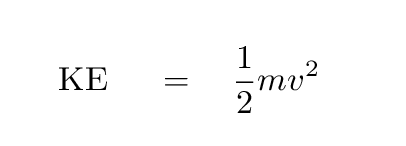
The SI units of energy are Joules:
Q: I toss a rubber ball of mass m = 0.2 kg
gently across the room at v = 5 m/s.
What is the ball's kinetic energy, in Joules?
Q: Crazy Ellie fires a 125-grain cartridge from
her Smith and Wesson .357 Magnum handgun
(one grain is approx 0.065 grams).
The bullet leaves the muzzle of the
gun at v = 440 m/s.
What is the bullet's kinetic energy, in Joules?
Sometimes, people use other units to describe energy. For example, if one measures mass in grams, distance in centimeters, and time in seconds -- the cgs system, which is sometimes used by astronomers -- then the units of energy are ergs.
High-energy physicists often use a unit of energy called the electron-Volt, or eV. If you let an electron accelerate across an electric potential of 1 Volt, then the kinetic energy it gains by the end of its journey is one eV.
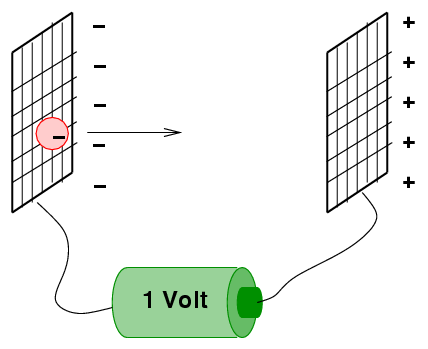
Q: The mass of an electron is 9.1 x 10^(-31) kg.
The velocity it gains by the time it reaches
the positive grid is about 593,000 m/s.
How many Joules are in one eV?
How many eV are in one Joule?
Q: I toss a rubber ball of mass m = 0.2 kg
gently across the room at v = 5 m/s.
What is the ball's kinetic energy, in eV?
The Large Hadron Collider at CERN will give
protons a kinetic energy of about 7 TeV.
a) which is larger: KE of rubber ball,
or KE of proton in LHC?
b) by what factor is the winner's KE larger
than the loser's KE?
Well, one of the most useful aspects of KE, and energy in general, is that one can SOMETIMES use it to solve very complicated problems in a simple way. In some situations, the mechanical energy of an object (or a system of objects) remains constant from start to end, no matter what complex paths it takes and no matter what sort of forces act on it. The mechanical energy is just the sum of KE and potential energy.
Consider a roller coaster ride. Bill and Ted (masses 50 and 70 kg, respectively) climb into the cars at the start of the ride. After they are strapped in, the cars shoot forward at speed v towards the first hill. As the cars roll up the hill, gravity pulls them straight down and the tracks push them up and to the left, in a constantly changing direction. It would be very difficult to account for the forces on the cars as they coast up the hill .... but energy makes the situation easy to analyze.
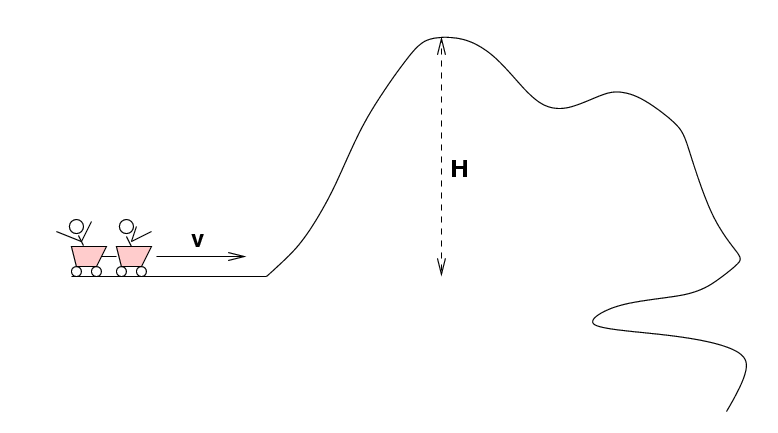
Q: If the hill is H = 100 feet tall,
how fast must the cars be moving to make
it up and over the hill?
Express your answer in miles per hour.
Well, no, not in general. The roller coaster was an example of the way that KE can be exchanged for gravitational potential energy and vice-versa. Although the total energy of a system of objects is always conserved throughout their interactions, the KE, by itself, is not.
However, there are occasional situations in which KE IS conserved. For example, when hard, solid balls -- like billiard balls -- collide, the kinetic energy before the collision may be the same as the kinetic energy afterwards. We call collisions in which KE is conserved elastic collisions. When high-energy physicists smash particles together in giant accelerators, they often see elastic collisions between sub-atomic particles.
Here's a less exotic example of an elastic collision: a baseball (m1 = 0.145 kg) thrown horizontally at v = 40 m/s strikes a stationary bowling ball (M2 = 6 kg) head-on.
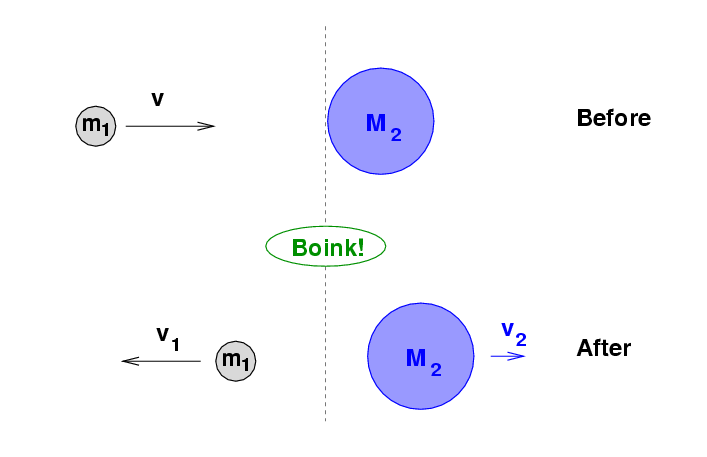
You will learn in University Physics I how to figure out the relationship between the initial and final velocities of balls in an elastic collision. It turns out that, in this particular situation, the result is pretty simple:
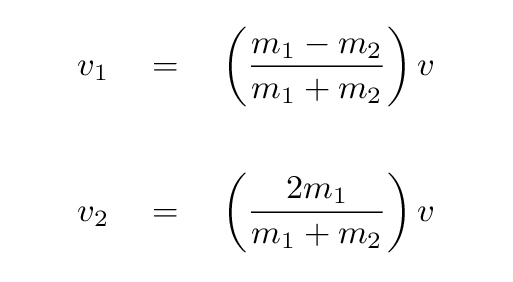
Q: What is the final speed of the baseball?
What is the final speed of the bowling ball?
What is the initial KE?
What is the final KE?
An invariant quantity is one that has the same value, no matter which observer is making measurements. The space-time interval
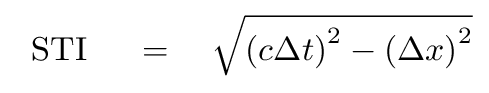
is an example of an invariant quantity.
Is kinetic energy an invariant quantity? Let's find out.
The Blue Man throws a ball (m = 0.2 kg ) at a speed of v = 20 m/s to the right.
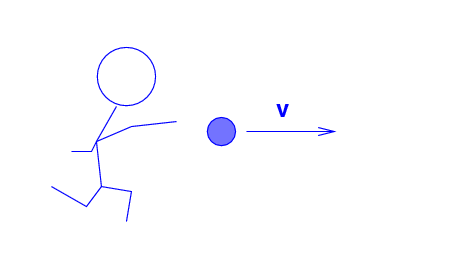
Q: What is the kinetic energy of the ball,
according to the Blue Man?
But the Blue Man and the ball are all travelling across the landscape at a speed of w = 50 m/s, as measured by the Red Men.
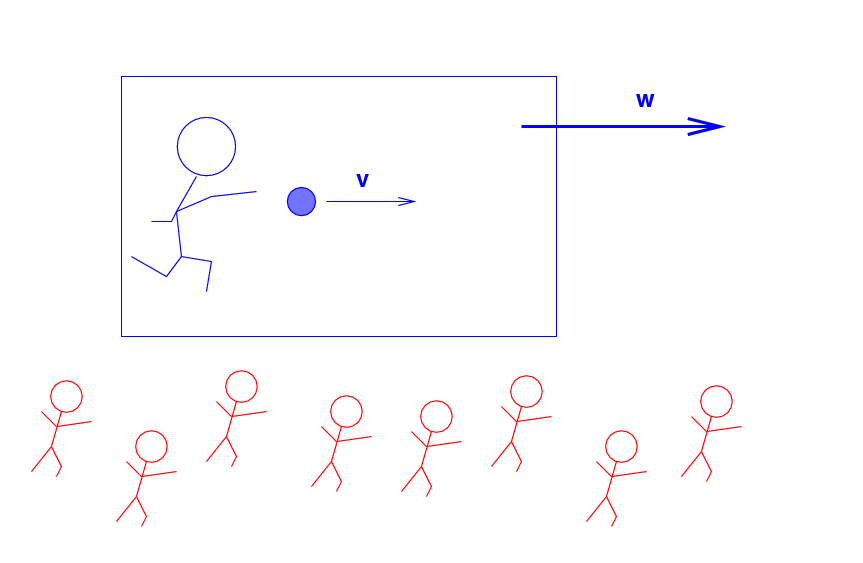
Q: What is the kinetic energy of the ball,
as measured by the Red Men?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.