Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
This is the second in a series on the "Twin Paradox".
Just to remind you of the important facts:
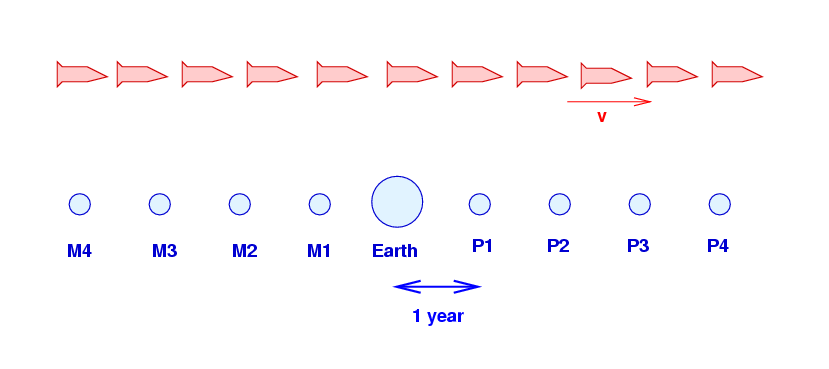
The Earth Federation has created a series of artificial planets stretching away in space in both directions. The planets are called "P1", "P2", "P3", etc., in the positive direction (right), and "M1", "M2", "M3" and so forth in the minus direction (left). Each planet is exactly one year (or light-year) from its neighbor in each direction.
The Federation Navy has a special fleet of red supply ships which travel through space with a constant speed v = 0.9c. There are many, many ships, all moving in a line, one after the other. These red ships keep their clocks synchronized with each other.
There is also a second fleet of green supply ships which travel through space in the OPPOSITE direction, moving with constant speed v = 0.9c. These green ships keep their clocks synchronized with each other (but not with the red ships).
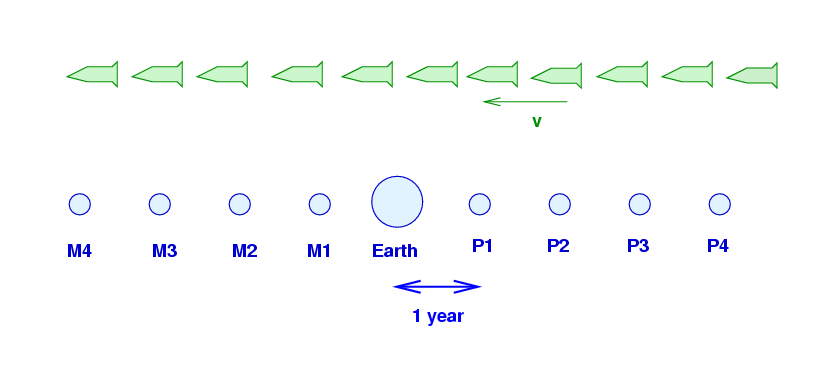
We won't talk much about the green fleet today.
Joe and Bob are twins living on Earth. On their twentieth birthday, Jan 1, 2500, Joe joins the Space Navy. He takes a shuttle into space to catch the Red Flagship, one of the Red Fleet ships. The clock on board that ship also reads Jan 1, 2500, as Joe climbs aboard.
Joe's plan is to travel to planet P27, then return home to Earth by switching to a green supply ship.
Joe and Bob agree that each will send his brother a "Happy Birthday" message once a year.
Let's analyze events by drawing a space-time diagram. We'll place the Earth at x = 0, and plot the position and time of events as measured by observers on the Earth (or any stationary planet). At the start of this story, Joe and Bob are both at location x = 0 (meaning the Earth) at time t = 0 (corresponding to Jan 1, 2500, on the Earth).
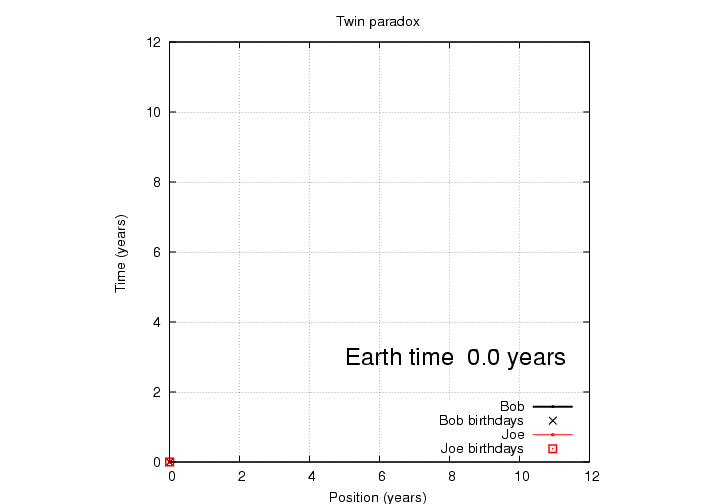
Click on the picture to see a
fast
animated version;
or
here for a slow
animation.
After one year passes on Earth, Bob sends a greeting into space. After another year passes on Earth, he sends another greeting. The messages travel at the speed of light c, and the ship is moving at v = 0.9c, so it takes a while for the messages to catch up to the ship.
Q: When does the first birthday greeting
catch up to Joe?
Express your answer in Earth years.
Express your answer in Joe's years.
"My twin is lucky," says Joe. "He is ageing much more slowly than I am."
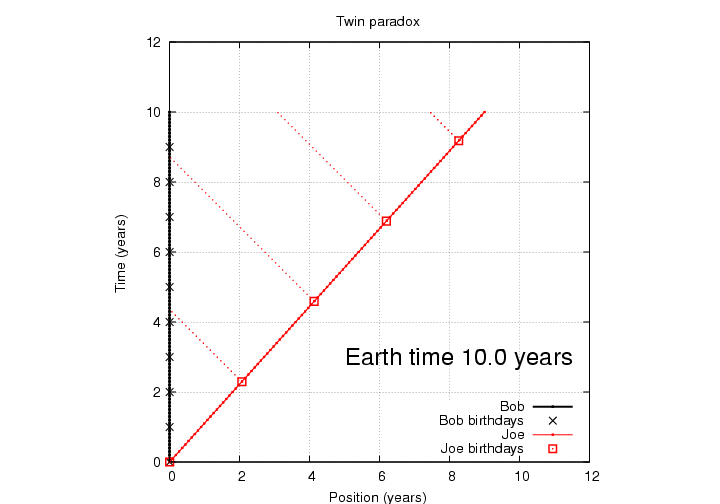
We can do a similar analysis by watching the progress of Joe's messages back to Earth. Joe sends one message each time he celebrates a birthday party on the ship.
Click on the picture to see a
fast
animated version;
or
here for a slow
animation.
Q: When does Joe's first birthday greeting
reach Bob back on Earth?
Express your answer in Earth years.
Q: When does Joe's second birthday greeting
reach Bob back on Earth?
Again, express your answer in Earth years.
"My twin is lucky," says Bob. He is ageing much more slowly than I am."
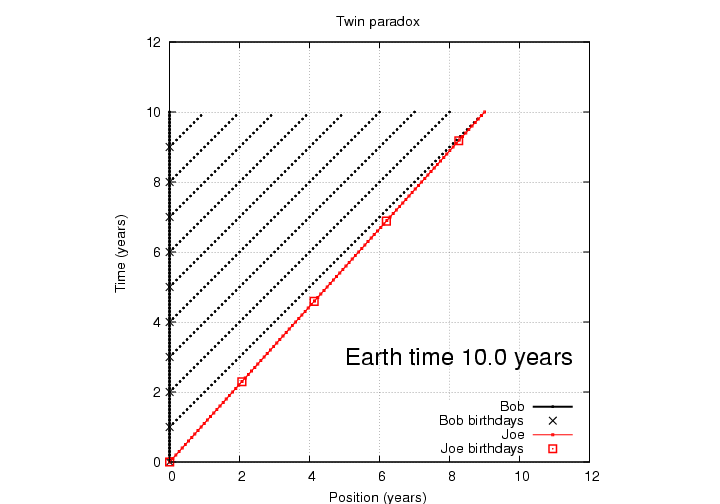
So far, each twin's experience is exactly the same: each ages 4.36 years between viewing successive birthday party messages from his brother.
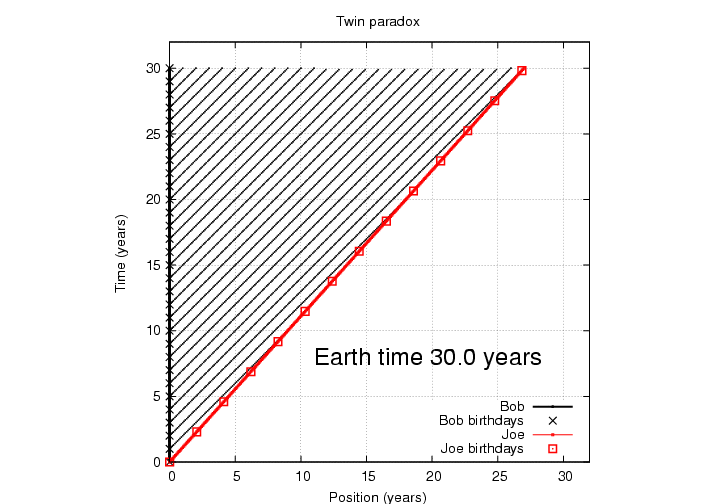
Q: How many of Bob's birthday parties does
Joe see by the time he reaches planet
P27?
Q: How old is Joe when he reaches Planet P27?
When Joe reaches planet P27, he is just over 33 years old. According to him, or any Red Navy ship, roughly 13.08 years have passed since he left home.
Joe takes a shuttle craft down to the planet very briefly -- just long enough to a little shopping -- and then immediately catches another shuttle onto one of the Green Navy ships. Joe is now moving at v = 0.9c in the opposite direction, back towards the Earth.
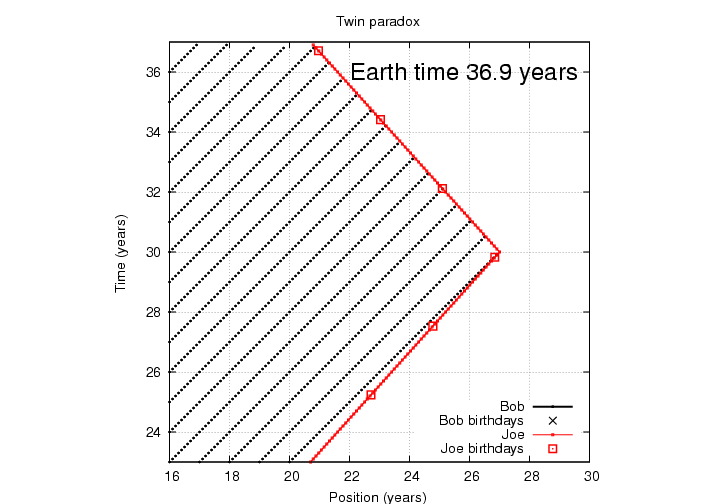
Things are very different now. Joe receives birthday messages from his brother on Earth with a very high frequency.
Click on the picture to see a
fast
animated version;
or
here for a slow
animation.
Q: How many of Bob's birthday
messages does Joe receive every
year now? That is, how many
messages per year in Joe's frame?
Joe is now receiving 4.36 messages each year; in other words, the interval between messages is only about 0.229 years.
"Wow!" says Joe, "My brother has changed from ageing slower than I do, to ageing much faster than I do."
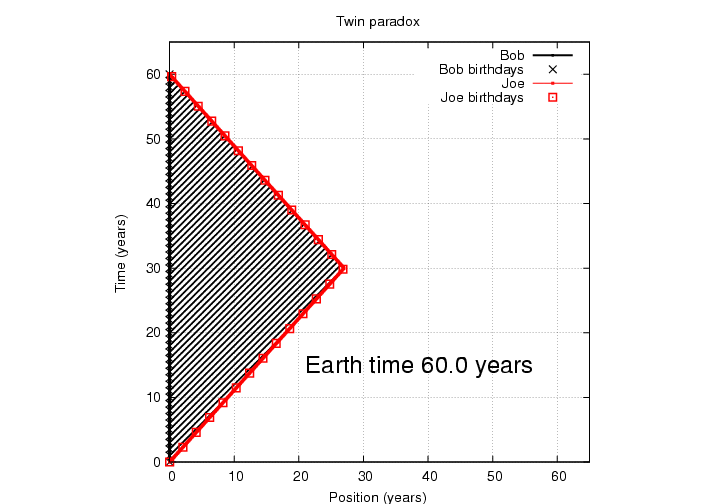
This rapid pace of birthdays continues during Joe's entire return trip to Earth.
Click on the picture to see a
fast
animated version;
or
here for a slow
animation.
Q: How many birthdays does Joe
celebrate during his return trip
to Earth?
Q: How many of Bob's messages
does Joe receive during his
return trip to Earth?
Q: According to Joe, how old
should Bob be when Joe lands
again on Earth?
Let's look at things from Bob's point of view. He sits at home during this entire trip. Every now and then, he receives a message from Joe.
Q: How frequently does Bob receive one
of Joe's messages?
Q: Bob turns 77; in other words,
57 years have passed since Joe
left. How many of Joe's messages
has Bob received?
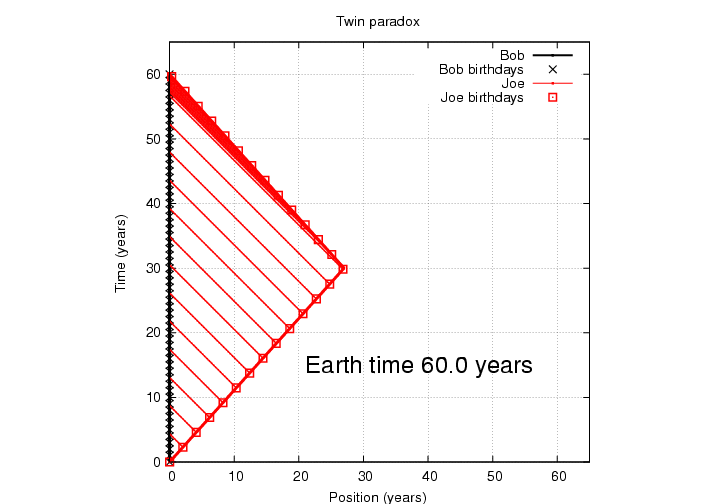
If we make a space-time diagram showing Joe's messages home during the entire journey, we can see what happens after Joe makes the turn at Planet P27 and heads back.
Click on the picture to see a
fast
animated version;
or
here for a slow
animation.
Just before Joe returns to Earth, a bunch of his birthday greetings arrive, one after the other, very rapidly.
"Wow!" says Bob, "My brother has changed from ageing slower than I do, to ageing much faster than I do."
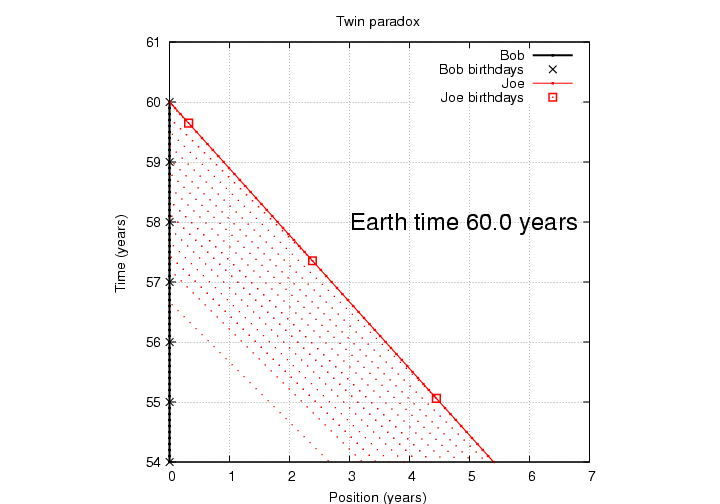
Let's zoom in for a closer look.
Click on the picture to see a
fast
animated version;
or
here for a slow
animation.
Birthday greeting number 13 (marking Joe's 33rd birthday) shows up at the usual time, 56.67 years after Joe left and 4.36 years after the previous message. But birthday greeting 14 (marking Joe's 34th birthday) appears somewhat early, and all the successive messages arrive at a rapid, constant rate.
Q: How many of Joe's messages does
Bob receive during a single one
of Bob's own years?
(Just look at the graph and count)
Q: How many birthday greetings arrive
at a rapid pace, before Joe himself
gets home?
Q: How old does Bob expect Joe to be,
based on the number of Joe's birthday
parties which he has seen?
The Andromeda Galaxy is about L = 2 million light-years away from the Milky Way Galaxy. You hear that the burgers in that galaxy are delicious.
Image courtesy of
Wikipedia and the Galaxy Evolution Explorer
So, you decide to make a round trip to the Andromeda Galaxy. The rules are:
Start: you are 20 years old End: you die when you reach 80 years old ship: travels at v = c - 1 m/s
Can you complete the trip before you die of old age?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
