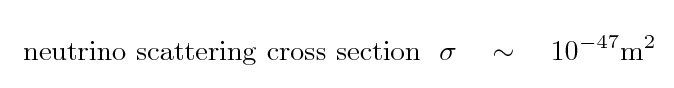
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Neutrinos are elusive: they hardly interact with matter at all. The cross section for interactions between a neutrino and a proton or neutron is very roughly (it depends on the energy of the neutrino)
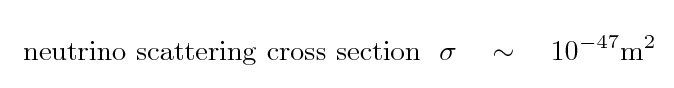
Let's try to figure out how far a neutrino typically moves through matter before it bumps into something; this distance is often called the mean free path. We'll start by calculating the volume the neutrino sweeps as it moves forward some distance L.
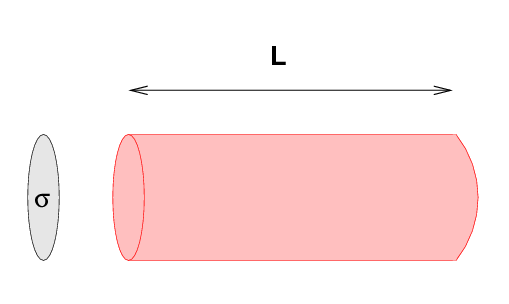
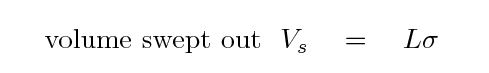
If the neutrino encounters one nucleon (a proton or a neutron) as it sweeps out this volume, then it will interact with the atom and we have a hope of detecting the neutrino. So, the question becomes, how many nucleons are there inside some volume?
Suppose we have a cube of material, exactly one meter on a side.
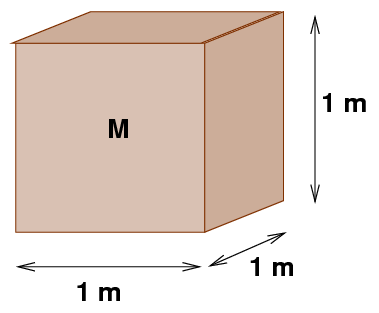
The mass of this cube is its density ρ times its volume:
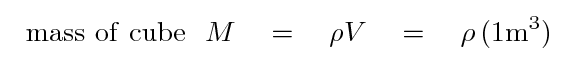
For simplicity, let's say that the mass of a proton is equal to the mass of a neutron, and let's also ignore the mass of the electrons in the cube. With these assumptions, the number of nucleons in this cube of material is simply the mass of the cube divided by the mass of a proton.
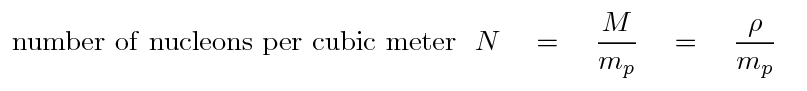
If we turn this upside down, we end up with the average volume occupied by each nucleon. Yes, yes, the protons and neutrons are all bunched together in the nucleus of atoms, with lots of space in between, but for statistical purposes, this will still work out.
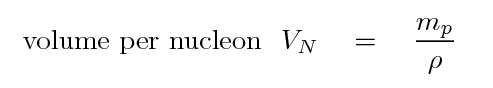
So, if the neutrino travels far enough, it will sweep out a volume equal to the typical volume occupied by one proton or neutron, and thus interact with the matter. We can therefore compute the typical distance the neutrino must travel before interacting L.
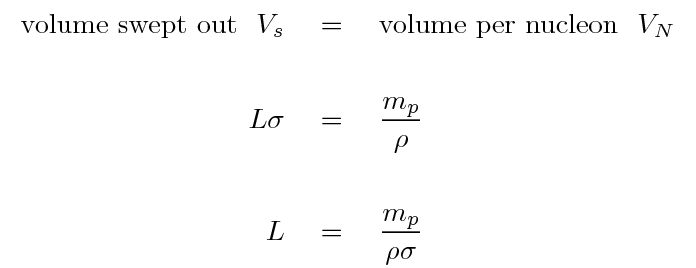
Q: Lead has a density of about 11,000 kg/m^3.
What is the mean free path of neutrinos through lead?
Q: How far does light travel in one year?
Holy cow!
How in the world can physicists hope
to detect neutrinos?
The basic idea is
The Super-Kamiokande neutrino detector in Japan is located in an old mine.
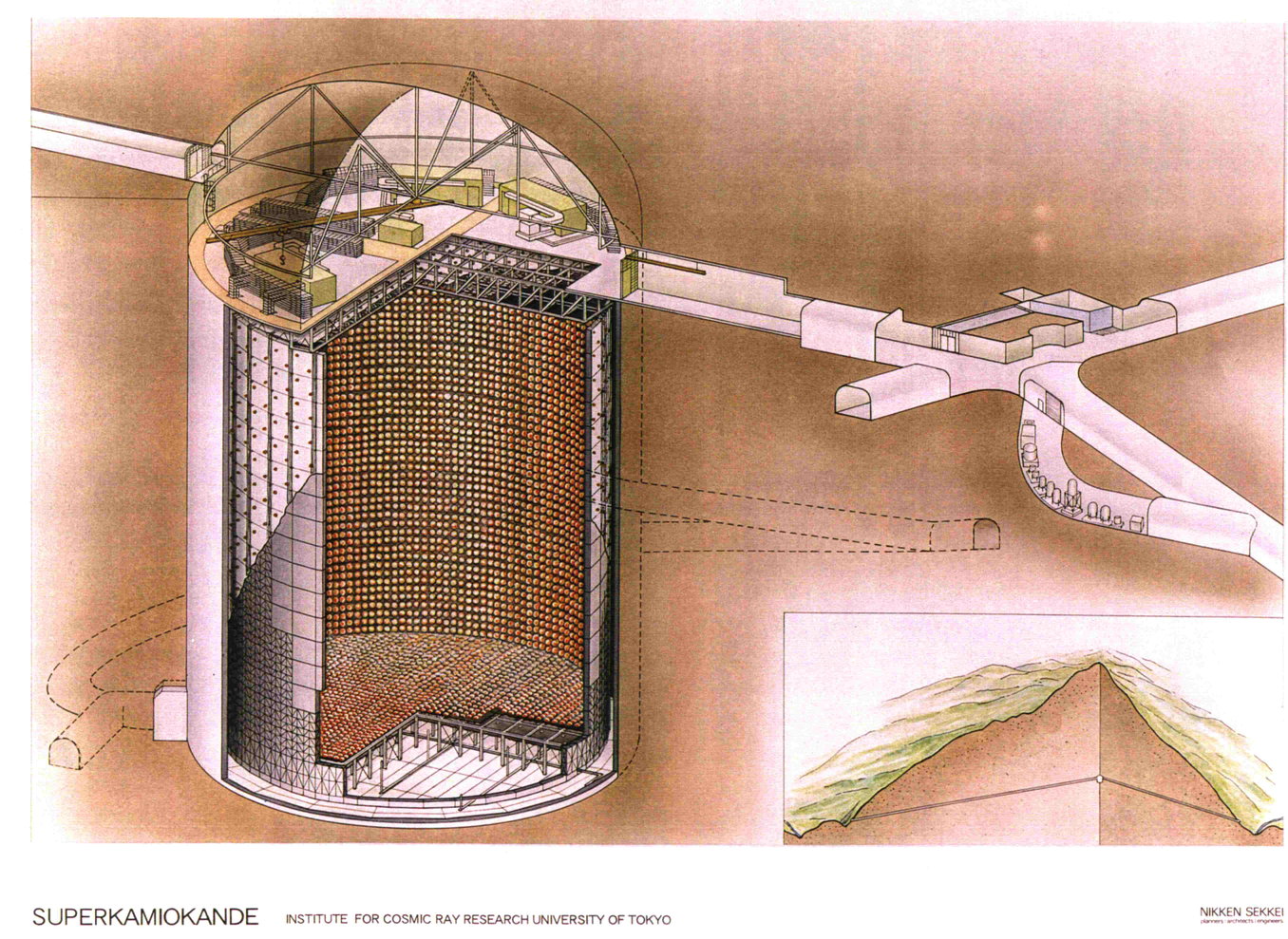
The pit walls are lined with photodetectors, which can sense short, faint pulses of light. There are a LOT of photodetectors. The pit is filled with very pure water.
You all know that no object with mass can travel at the speed of light IN A VACUUM, right? Right. But if you consider situations other than a vacuum -- for example, a big tank of water -- it turns out that objects CAN move faster than light inside that medium. The speed of light inside a medium is slower than c by a factor called n = index of refraction for the material. For water, n = 1.33, so
c
speed of light in water = ------- = 225,000,000 m/s
1.33
A sufficiently violent process can shoot a particle through water faster than this speed. If that particle is electrically charged (like an electron or a proton, but not a neutrino), the particle will emit light as it moves through the water.
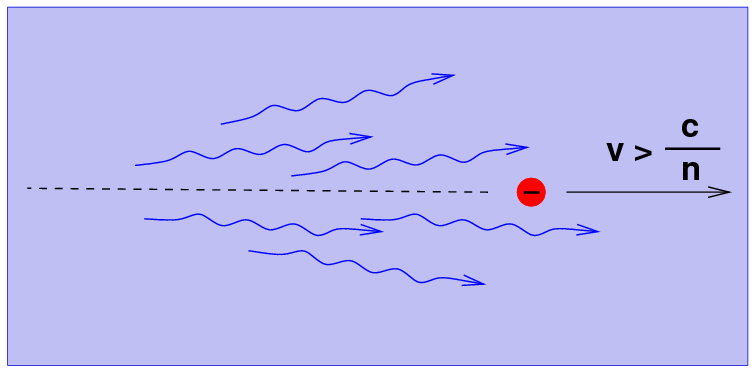
The Cerenkov light has two characteristics:
The eerie blue glow you may see in pictures of a nuclear reactor is Cerenkov radiation.
Image taken from
http://www.spectrum.ieee.org/image/37182
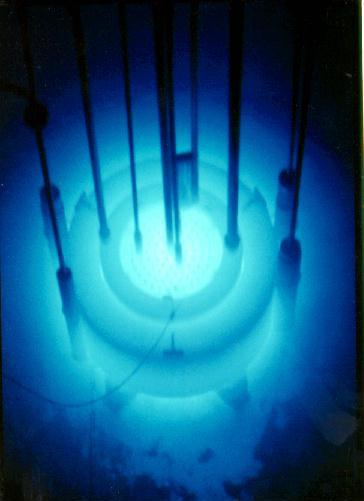
Photo by Jeffrey Bradford
So, if a charged particle flies through the water of the Kamiokande detector at superluminal speeds, it will emit faint blue light in the direction it is travelling. The light can be sensed by the photodetectors on the walls of the mine, and the result allows physicists to figure out both the energy of the particle and the direction whence it came.
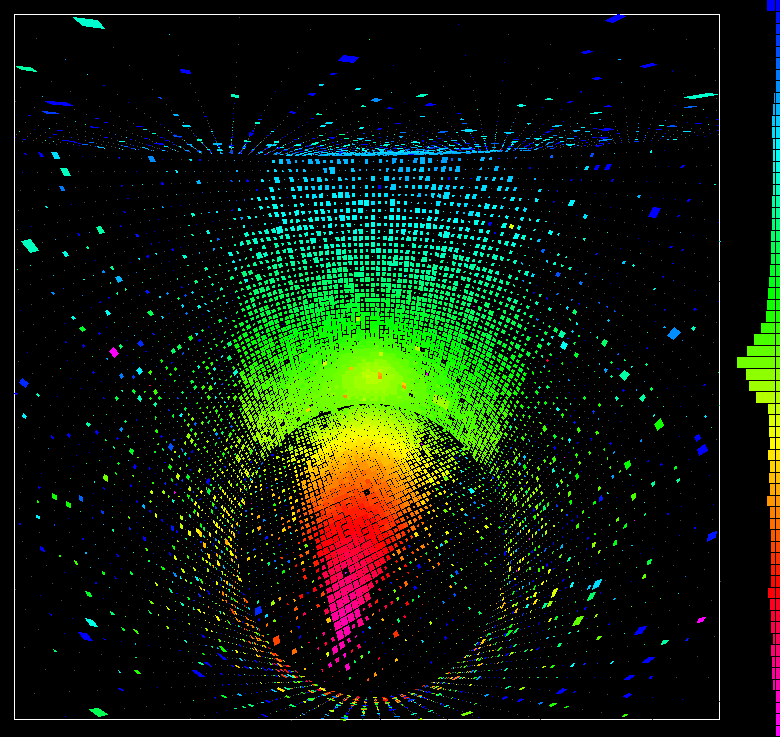
Example of a muon event at Super-Kamiokande.
Pink = early detections, green = later detections.
Even with a mine over 50 meters high, holding 50,000 tons of water, the rate of neutrino events is still pretty low. The strongest source of neutrinos, the Sun, yields only about 9 events each day! The scientists have to wait for years to build up statistically significant samples to test various theories.
Is there a better, faster way? YES -- build a much larger detector. But how?
The Ice Cube is a giant Cerenkov detector which uses the frozen water of the Antarctic ice cap to provide a massive target for neutrinos. It is much, much bigger than Super-Kamiokande.
Of course, this does mean that the scientists have to bring warm gloves.
The team drills holes more than a mile deep into the ice.
Then they lower a long string of photodetectors into the hole.
The ice deep beneath the surface at the South Pole is very pure, and very transparent. Cerenkov radiation will travel many meters through the ice, allowing many of the detectors in different strings to sense the light from a single event.
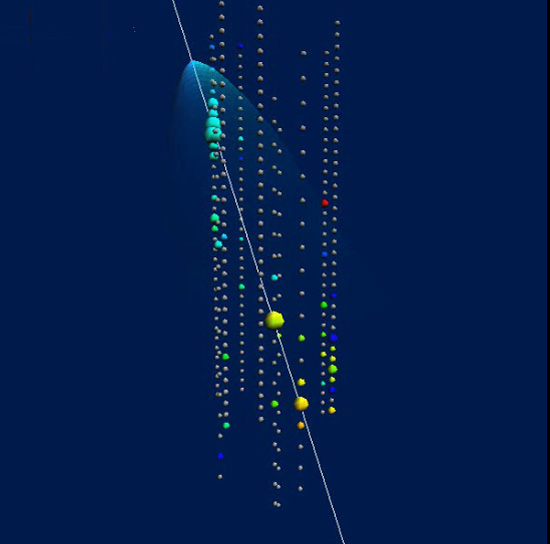
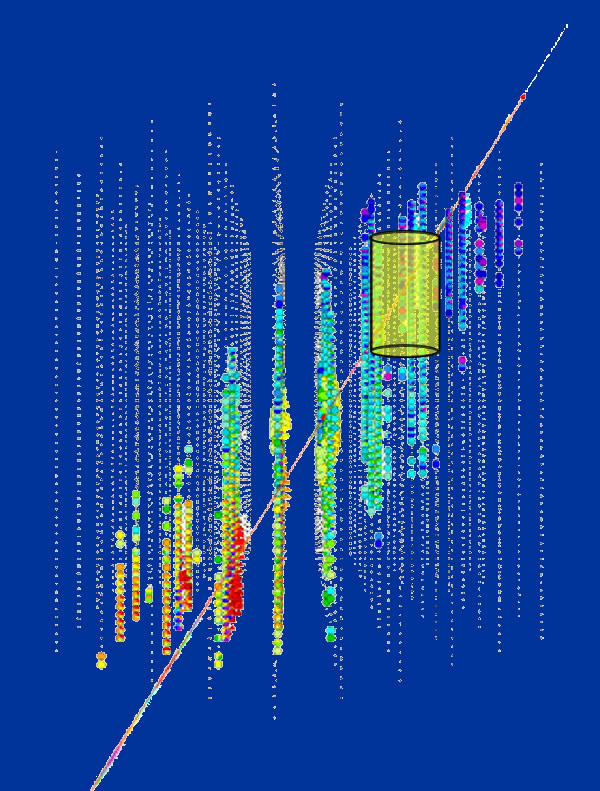
The ability of IceCube to determine the direction of the energetic particles is very important. It turns out that neutrinos aren't the only particles which produce Cerenkov light inside these giant detectors; muons can also travel through the Earth's atmosphere and several miles of dirt and rock to interact with the ice.
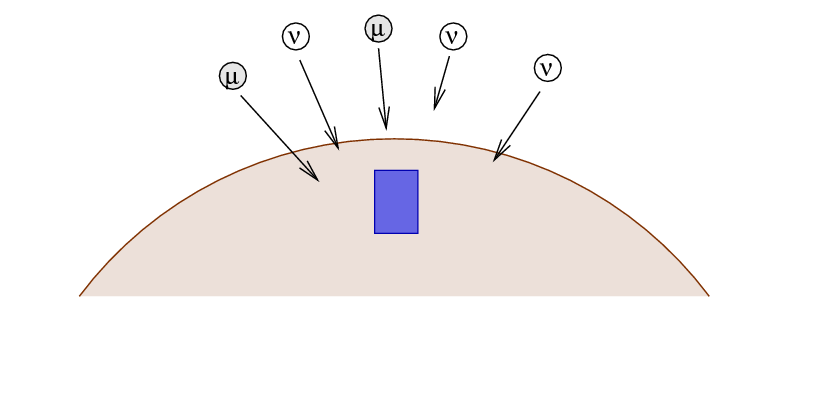
However, if one detects a particle which enters the detector from below, then it's obvious that it must be a neutrino: no other particle can travel through the entire Earth and reach the detector from below.
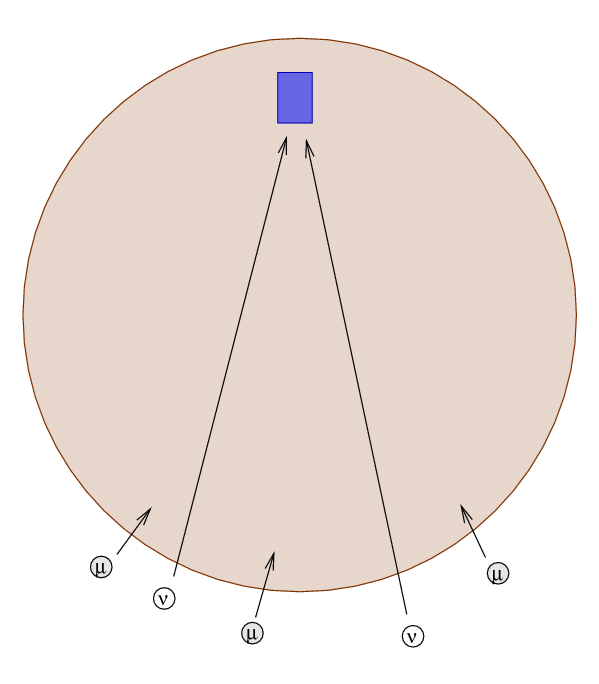
Q: The radius of the Earth is about 6.37 x 106 meters.
The mass of the Earth is about 5.98 x 1024 kg.
What is the average density of the Earth?
Q: What is the probability that a neutrino will interact
with a proton or neutron as it travels all the way
through the Earth?
The image below shows the detection of a high-energy neutrino on Nov 12, 2010. Click on the image to see the animation on Youtube.
Animation courtesy of
the Ice Cube Neutrino channel
So, determining the direction of the particle allows physicists to cut down on the background noise due to other particles. In addition, it will allow them -- after the IceCube array becomes fully operational for several years -- to build up map of the sky, showing the locations of strong neutrino sources. This is a simulation of what the scientists might see ....
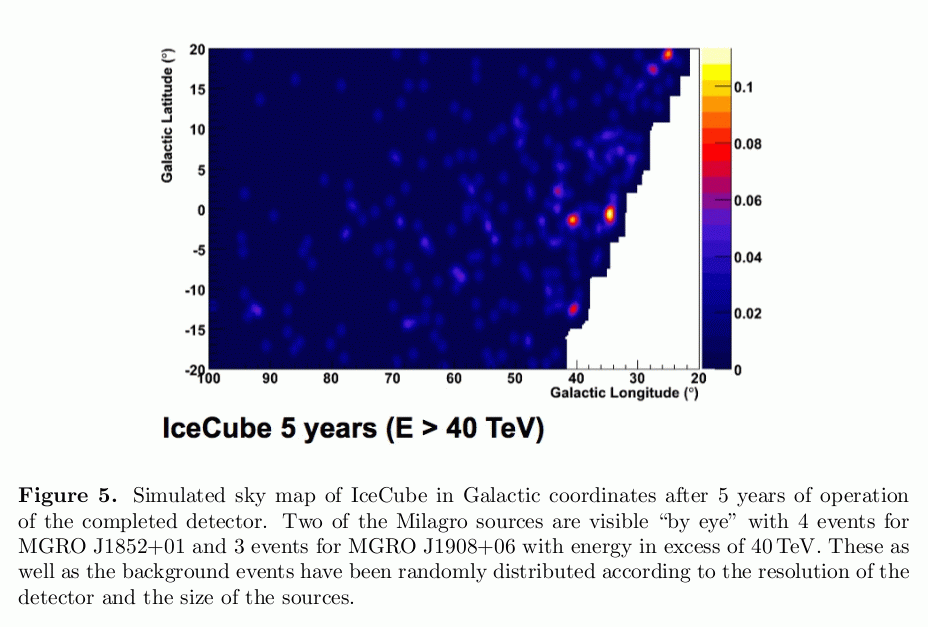
Taken from Halzen, "IceCube Science", Journal of Physics Conference Series 171 (2009)
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.