Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Spoiler alert: today's lecture discusses methods for finding planets around other stars which haven't produced much success so far.
What could be so hard about it? Just point your telescope at a star, take a picture, and look for little dots of light around the star. Right?
Well, there are a few complications. Namely,
Let's consider each one of these points.
The first one is pretty simple: stars are big, and planets are small. Even if all else were the same, planets would be much fainter.
Sources for these images can be found at
http://spiff.rit.edu/classes/resceu/ss_planets/earth_moon_lineup.html
How much fainter would a planet be, due simply to this size difference? You can get a qualitative feeling for the answer by looking at the picture below, which shows an ordinary star (Sirius) next to an unusually small, planet-sized star (Sirius B).
Image courtesy of
NASA, ESA, H. Bond (STScI) and M. Barstow (University of Leicester)
But let's get a quantitative estimate for the "size" factor. Suppose that the Earth were a tiny star, with the same temperature as the Sun. The difference in their brightness would be
Given the sizes of the Earth and Sun
radius of Sun RS = 6.96 x 105 km
radius of Earth RE = 6.37 x 103 km
what would this ratio of brightness be?
That sounds ... pretty dim, by comparison. Could we see such a dim little spot of light next to an ordinary star?
Astronomers measure the sensitivity of their instruments -- the ability to detect a faint little point source next to a very bright point source -- in terms of the contrast between the two objects. That means, basically, the ratio of their brightness. The farther apart the two sources are, of course, the easier it is to see the faint one.
Below are graphs showing the performance of two of the best planet-finding cameras available today. The first is the Gemini Planet Imager . Suppose that our imaginary star-like little planet were located 1 arcsecond away from its host star. Could GPI see it?
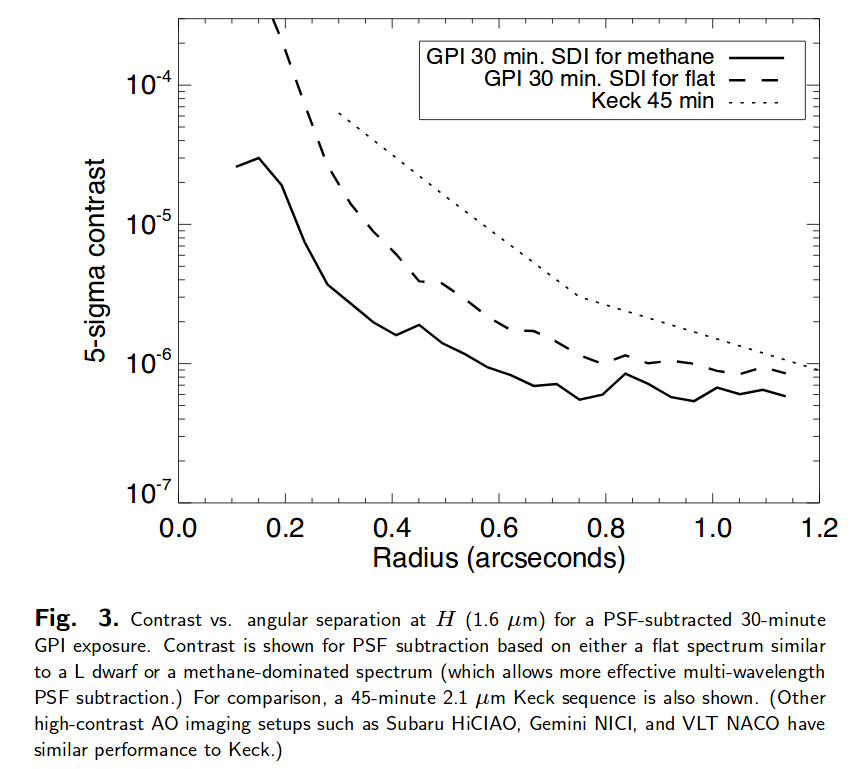
Figure 3 taken from
Macintosh et al., PNAS 11112661 (2014)
Another instrument designed to find planets is SPHERE, which is mounted on one of the VLT units in Chile. Could SPHERE see our imaginary little planet?
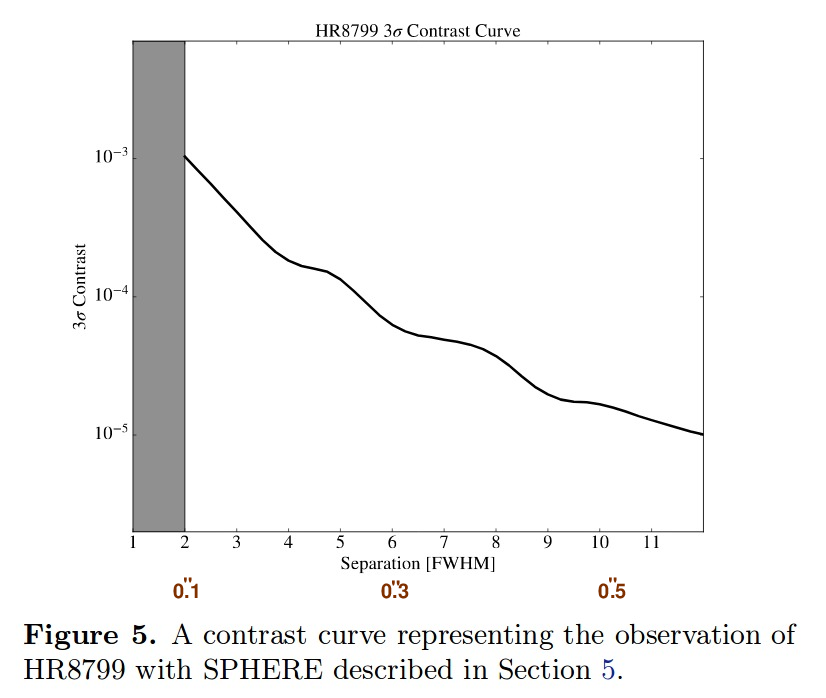
Figure 5, with annotations added, taken from
Jensen-Clem et al., AJ 155, 19 (2018)
Sounds like no problem, right? But we've only mentioned one of the factors which makes planets hard to find (size). We must also taken into account the fact that (most) planets don't radiate profuse amounts of light, like stars do. Instead, most planets shine only by reflected light. As light from the star flies out into space, only a teeny-tiny fraction of that light happens to strike the planet and bounce off.
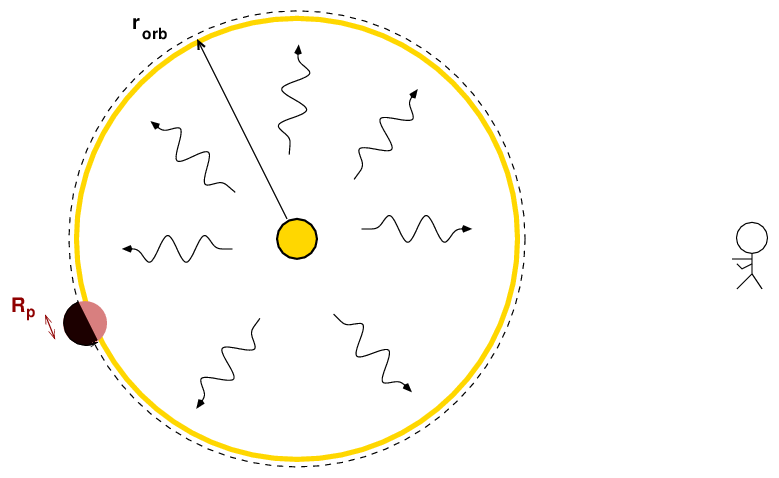
So, in order to compute the brightness of the planet to that of its host star, we need to compare the size of the planet to the size of a sphere with the planet's orbital radius -- because the light from the star is spread out over the surface of this giant sphere when it reaches the planet.
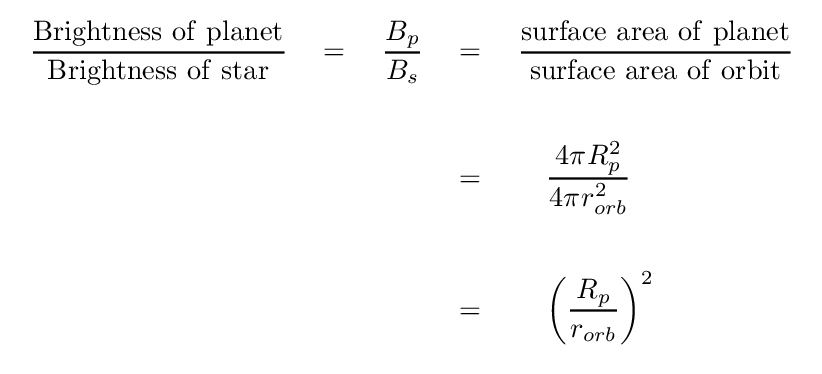
Given the sizes of the Earth and its orbit
radius of Earth's orbit RS = 1.50 x 108 km
radius of Earth RE = 6.37 x 103 km
what would this ratio of brightness be?
Q: Can our current instruments detect an Earth-like planet
orbiting at an Earth-like distance from a Sun-like star?
Nope. It isn't even close.
And yet ... and yet ... astronomers HAVE detected several planets circling other stars, simply by taking pictures of them.
How did they take such pictures???
The answer is that these pictures show
For example, consider the planet around the star HD 95086. Below is a set of four images, showing the star (HD 95086) and the planet (HD 95086 b) at infrared wavelengths of 1.6 micrometers (H) and 2.2 micrometers (K).
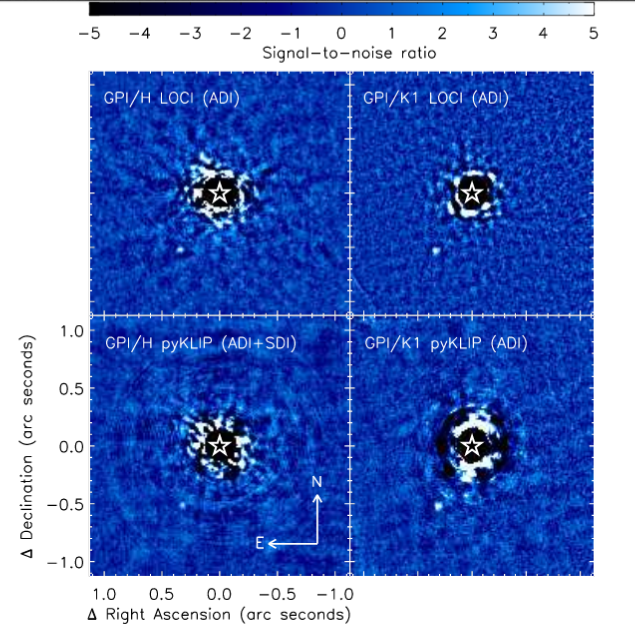
Figure 1 taken from
DeRosa et al., ApJ 824, 121 (2016)
The central region of these images looks dark because a model of the very, very bright star has been subtracted away; that allows faint objects to be seen. The little dot near the 7 o'clock position in these images is the planet. It may look like a tiny little dot, very close to its star; but the actual parameters show that this planet is far from an Earth-like world.
Clearly, this is NOT a planet you would enjoy visiting.
But wait a minute. The planet is far, far from its host star, and yet also very hot. How is that possible? Is the host star extremely luminous? No, it actually radiates less energy than the Sun.
Q: How in the world can the planet HD 95086 b have a
temperature of around 1000 Kelvin, yet orbit
more than 50 AU from its host star?
The answer is that this system, star and planet, is still very young. DeRosa et al. (2016) estimate that the system is only about 17 million years old. While that's a long time for a person, it's only a short span of time on a planetary time scale. Because the planet formed so recently, the internal heat of its creation (all those giant impacts of planetesimals, for example) is still leaking out.
So, direct imaging is not one of the most efficient methods of finding planets around other stars. As a matter of fact, as of Nov 12, 2018, only 44 out of 3837 (1.1%) confirmed exoplanets have been discovered in this manner.
You are familiar with the Big Dipper, right? The dipper shape is just a temporary one. If you wait a few thousand years, it will change; and in a hundred thousand years, change drastically. Just click the picture to see ...
Image created with
Tony Dunn's proper motion simulator. Thanks, Tony!
What's going on? Each star we see in the sky is a member of our Milky Way Galaxy. All stars are orbiting around the center of the Galaxy, with a wide range of speeds, distances, and directions. That means that as our Sun moves, and those stars move, we on Earth with see the stars drift slowly across the sky.
Suppose that we choose one star -- just one -- and measure its position very carefully for several decades. We ought to see it progress in some direction at some speed, in a path which is (to a very good approximation) just a straight line.
But suppose that this star was not alone. Suppose that it had a big, massive, planet, 100 times the mass of Jupiter, orbiting around it at a distance of 1 AU.
Yes, yes, I know that an object with 100 times the mass of Jupiter would be a star, not a planet, but let me use this value for ease of illustration.
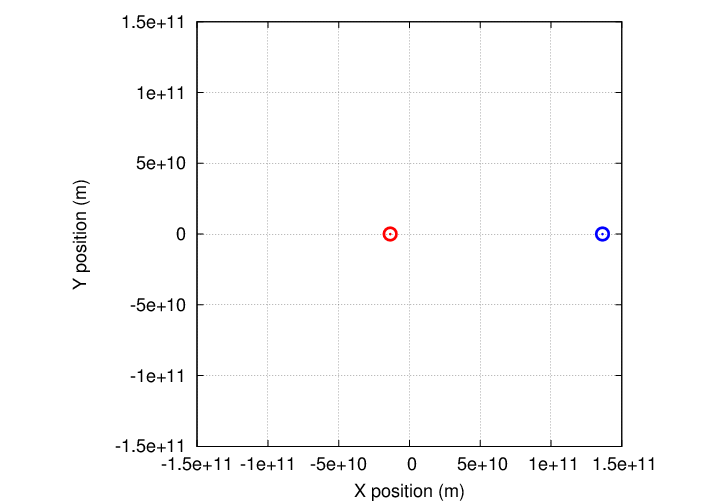
If we could watch this system from a vantage point far above it over several decades, we'd see that the planet moves in an orbit ... but that the star ALSO moves in an orbit with the same period. Both the star and planet would move around their common center of mass.
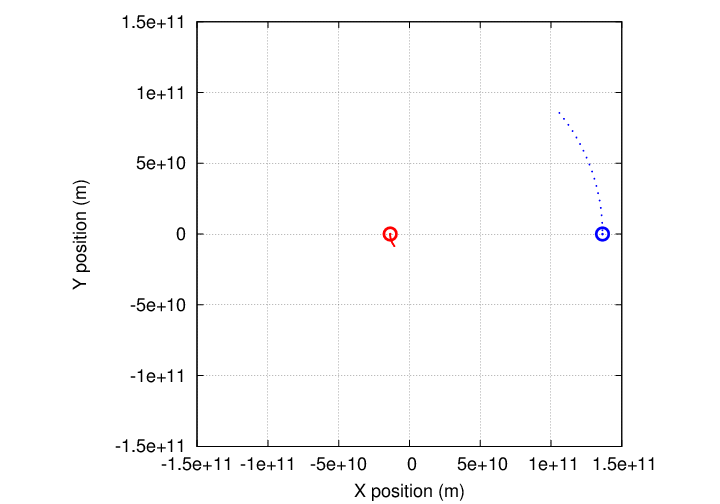
The size of each orbit depends on the mass of each partner.
property star planet ratio (star/planet)
------------------------------------------------------------------------
mass 1 0.1 10
dist to center of mass 1 10 0.1
circumference of orbit 2 pi 20 pi 0.1
period 1 1 1
speed of motion 2 pi 20 pi 0.1
------------------------------------------------------------------------
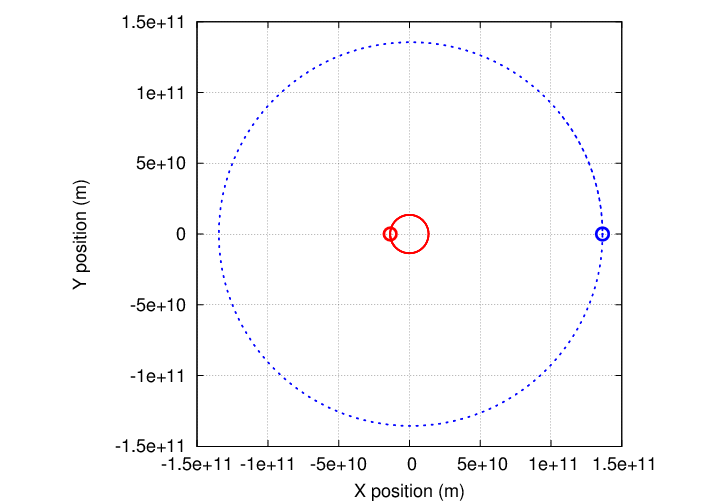
So, if we had a bird's-eye view, looking down on the star-plus-planet binary from a fixed point in space, we'd see the star move in a little circle over many years, and the planet move in a bigger circle over the same number of years.
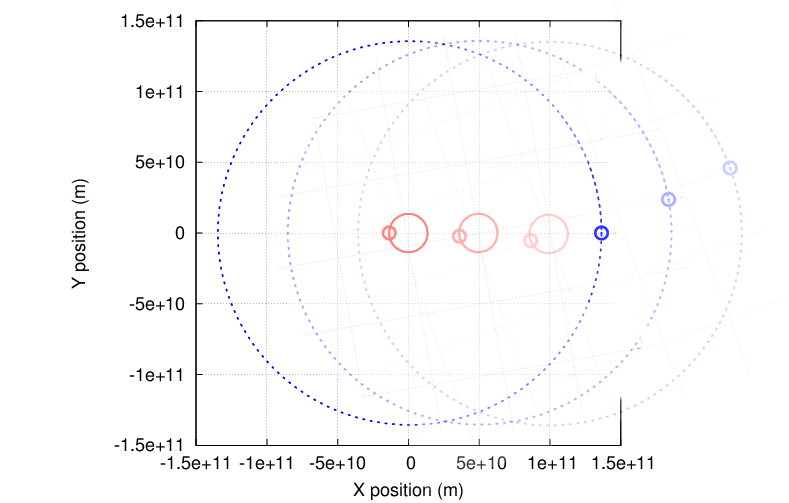
But what if we were watching from another location? What if we were watching from some other star? Then the proper motion of the star-plus-planet binary system would cause it to slide across the sky at the same time that the star, and the planet, appeared to orbit around each other. The result would be complicated ...
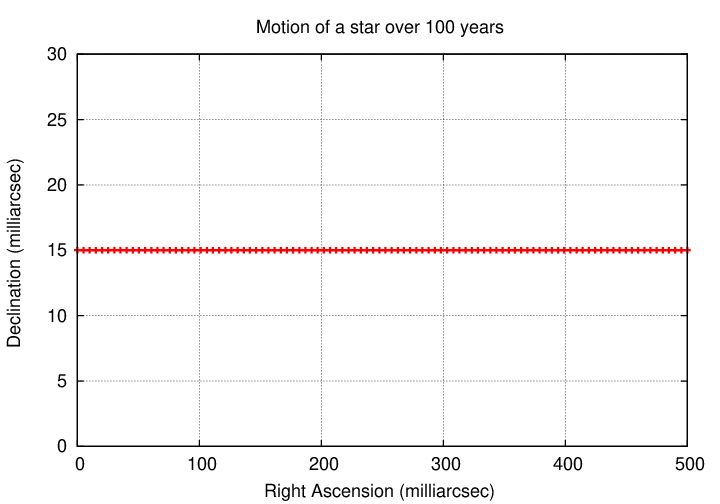
So, let's begin by observing a star which is completely alone in space. It simply moves across the sky in a straight line as the years go by. Simple, yet boring.
If, instead, we observe a system which contains both a star and a massive planet, we'll see both the star and the planet wiggle back and forth as they slide across the sky. The planet's wiggles are larger in size, because its orbit is larger than the star's orbit.
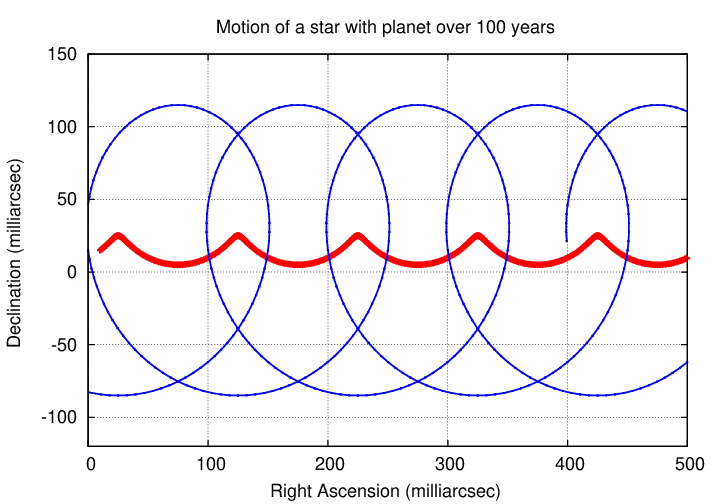
In most cases, any planet will be so much fainter than its host star that we can't see it. Thus, what we might observe is the star alone, but moving in the same distinctive wiggly path.
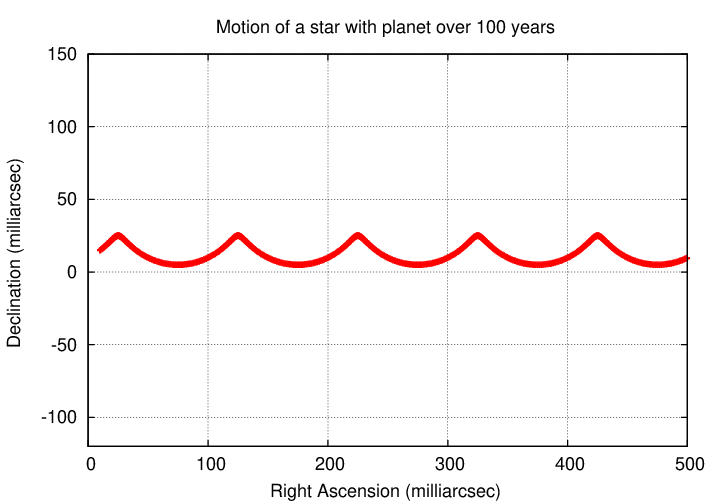
These wiggles will be very, very, very small, in most cases, but if we can perceive them, then we can deduce that the star must be accompanied by a companion. If we can measure the size and period of the wiggles, we can figure out some of the companion's properties.
This method has worked in the past. The star Sirius, the brightest star in the night-time sky, is so close to our Sun that it appears to move very quickly across the sky. In 1844, astronomer Friedrich Bessel noticed small oscillations in its path and deduced that it must have a companion orbiting around it.
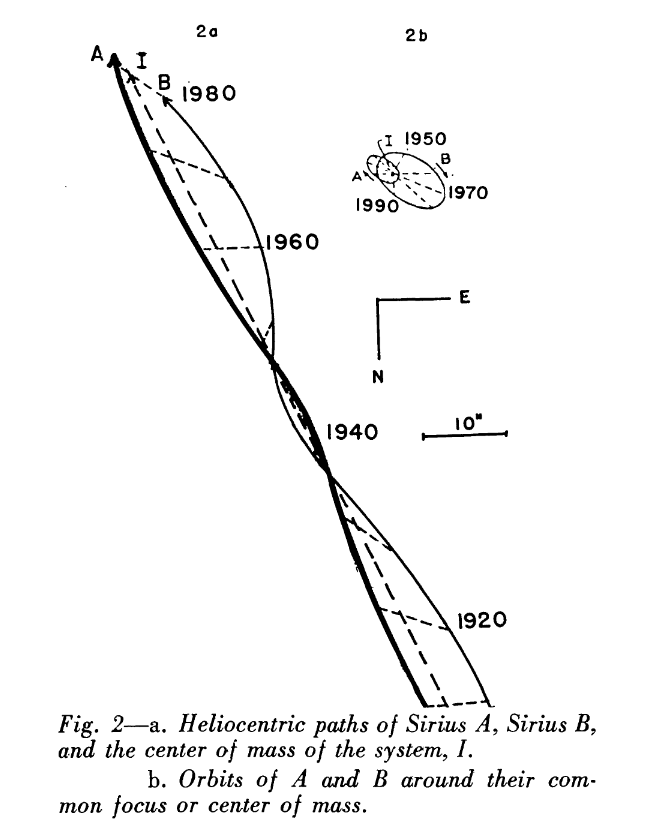
Image taken from
Lippincott, Astronomical Society of the Pacific Leaflet 8, 311 (1961)
Now, the companion of Sirius is a star, not a planet; it has a mass slightly larger than our Sun, and so exerts a very large gravitational force on Sirius itself. That makes the motion of Sirius relatively easy to detect: it has an amplitude of about 3 arcseconds.
But if we are looking for evidence of a PLANET causing wobbles in the motion of a star, we must be ready to detect much smaller motions. Even Jupiter has a mass of only about 1/1000 of the Sun, which means that we might expect wiggles with amplitudes of about 1/1000 that of Sirius; perhaps only milli-arcseconds in size. That means that one must make very, very, very careful measurements.
Back in the early 1900s, astronomer Peter van de Kamp did make very careful measurements of stellar positions. He used the 61-cm Sproul refracting telescope at Swarthmore College to take photographs of many stars, including Barnard's Star.
Image courtesy of
Amazon.com
Over the period 1938 to 1968, he found small variations in the position of Barnard's Star relative to reference stars. It wasn't moving in a straight line through the sky, but in a wiggling path:
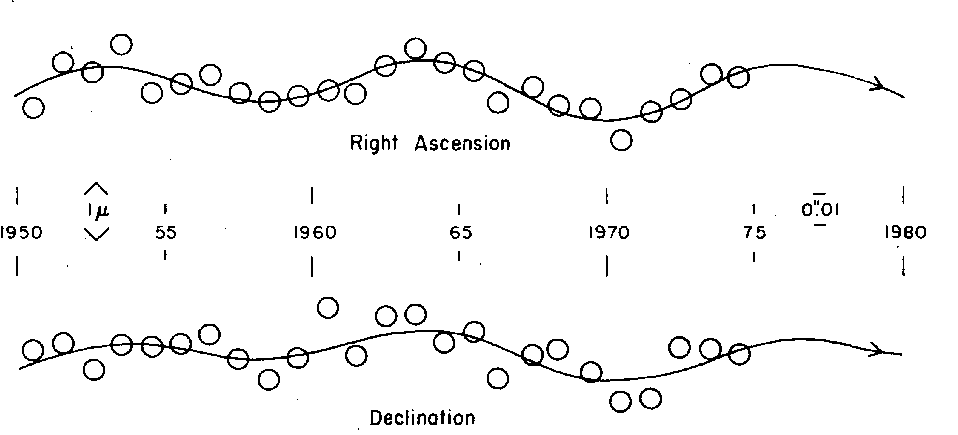
Figure taken from
van de Kamp, AJ 80, 658 (1975)
Van de Kamp attributed these wiggles to the gravitational influence of two planets with pretty long orbital periods:
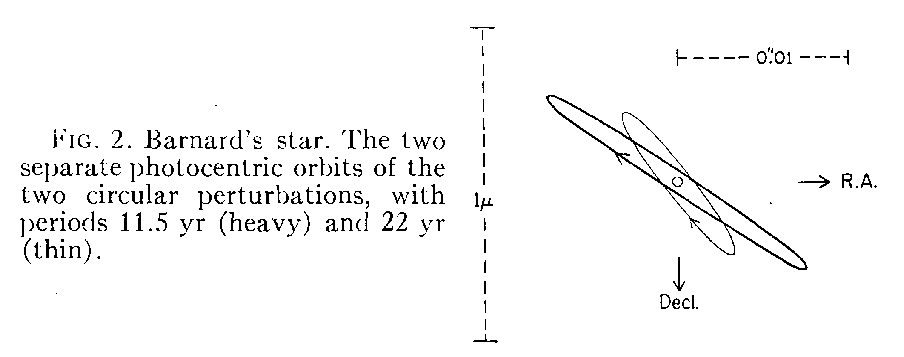
Figure taken from
van de Kamp, AJ 80, 658 (1975)
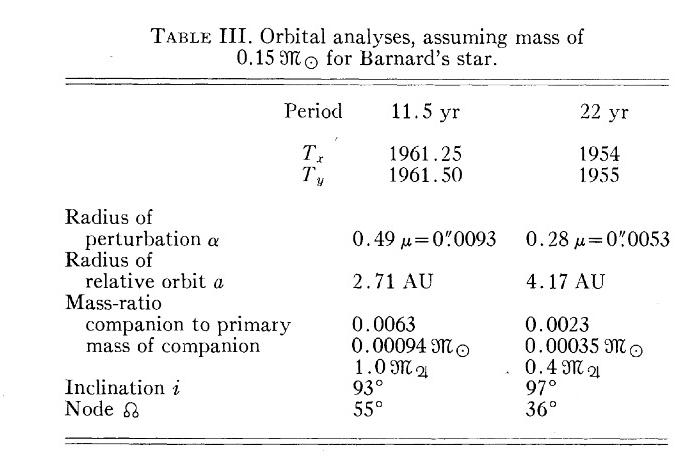
Figure taken from
van de Kamp, AJ 80, 658 (1975)
Q: What are the sizes of the motions of the star due to
each of the claimed planets, in milli-arcseconds?
Needless to say, measuring such small changes in the position of a star is hard. Really hard. No other observatory could reproduce these results (but very few tried, since it takes so long). Other astronomers raised some concerns about the measurements of these plates from the Sproul refractor.
In the late 1990s, astronomers used the Fine Guidance Sensors on HST to measure the position of Barnard's Star over a five-year period.
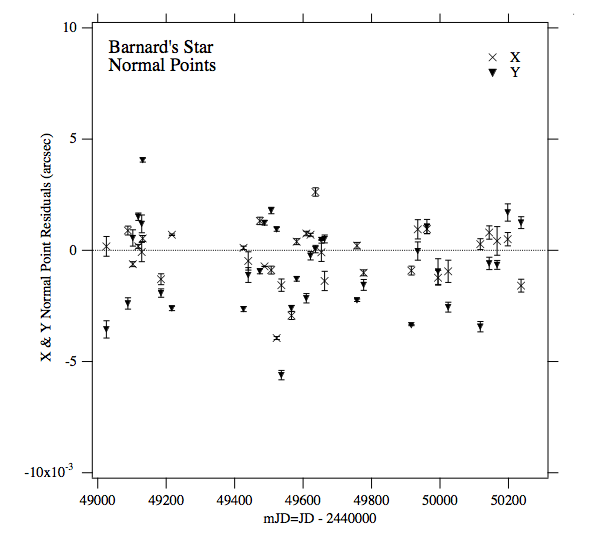
Figure taken from
Benedict et al., AJ 118, 1086 (1999)
Q: How large should the claimed motion of Barnard's Star
appear on this graph?
Alas, in this particular case, it appears that the search did not yield a planet.
And, in general, the astrometric method of planet discovery is so hard that very few planets have been found this way. Only 1 in 3837 confirmed planets in NASA's Exoplanet Archive is listed as being discovered via astrometric measurements.
Oh, and I've been describing a simplified version of the motion of a star across our sky. In real life, stars which are close enough for us to detect wobbles due to their planets will also show periodic motions due to parallax, as the Earth orbits the Sun. If you can want to see some of the gory details, you can read this lecture from another class.
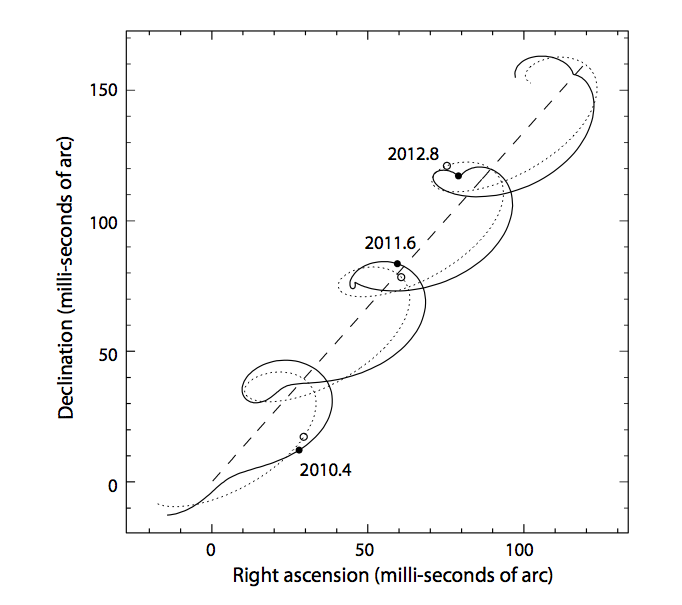
Figure 2 taken from
Perryman (European Physical Journal H, 37, 745 (2012))
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.